组合总数IV

发表于
本文字数： 1.3k 阅读时长 ≈ 1 分钟

LeetCode每日一题，377. 组合总数 IV

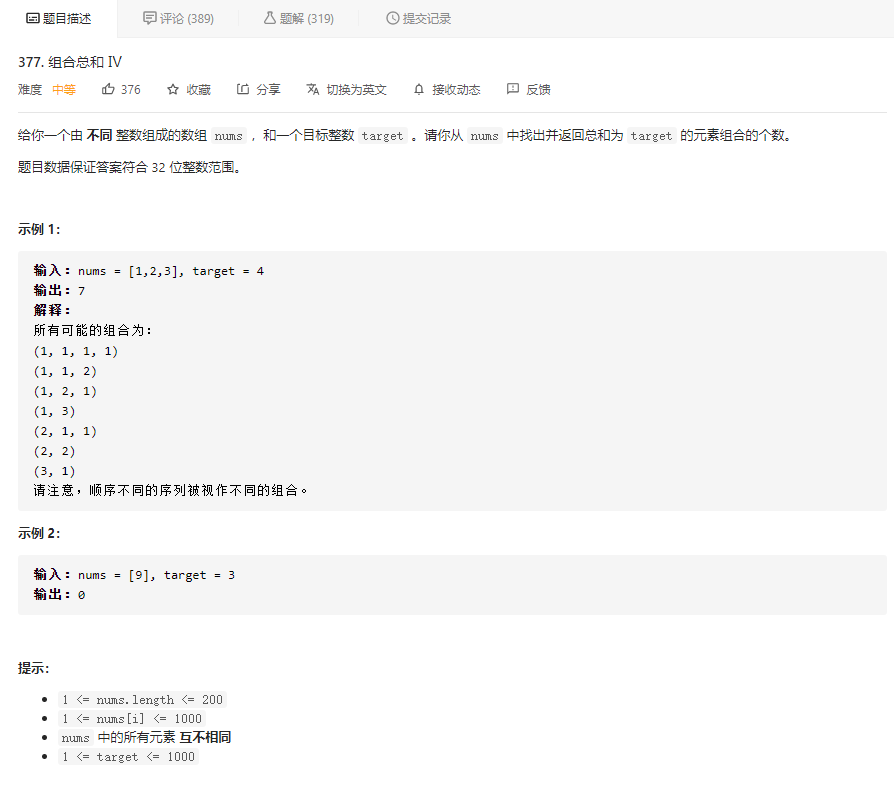
先看题目描述

cvCXtJ.png

算法和思路

动态规划

定义状态方程 dp[i] 表示选取的元素之和等于 i 的方案数，边界是 dp[0] = 1，只有不选取任何元素时，元素之和才为 0，因此只有一种方案

当 1 <= i <= target 时，对于数组 nums 中的每个小于等于 i 的元素 num，只要在元素之和等于 i - num 的排列最后添加 num，即可得到一个元素之和等于 i 的排列，因此在计算 dp[i] 时，应该计算所有 dp[i - num] 之和

算法流程：

  • 初始化 dp[0] = 1
  • 遍历 i 从 1 到 target，对于每个 i：
    • 遍历数组中的元素 num，若 num <= i，将 dp[i - num] 的值加到 dp[i] 上
  • 最后返回 dp[target]

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public int combinationSum4(int[] nums, int target) {
        int[] dp = new int[target + 1];
        dp[0] = 1;
        for (int i = 1; i <= target; i++) {
            for (int num : nums) {
                if (num <= i) {
                    dp[i] += dp[i - num];
                }
            }
        }
        return dp[target];
    }
}

下面是一开始实现的一个 dfs 的代码，跑的超时了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    private int res = 0;

    public int combinationSum4(int[] nums, int target) {
        dfs(nums, 0, target);
        return res;
    }

    private void dfs(int[] nums, int cur, int target) {
        if (cur == target) {
            res++;
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            if (cur + nums[i] <= target) {
                dfs(nums, cur + nums[i], target);
            }
        }
    }
}