最大整除子集

发表于
本文字数： 1.4k 阅读时长 ≈ 1 分钟

LeetCode每日一题，368. 最大整除子集

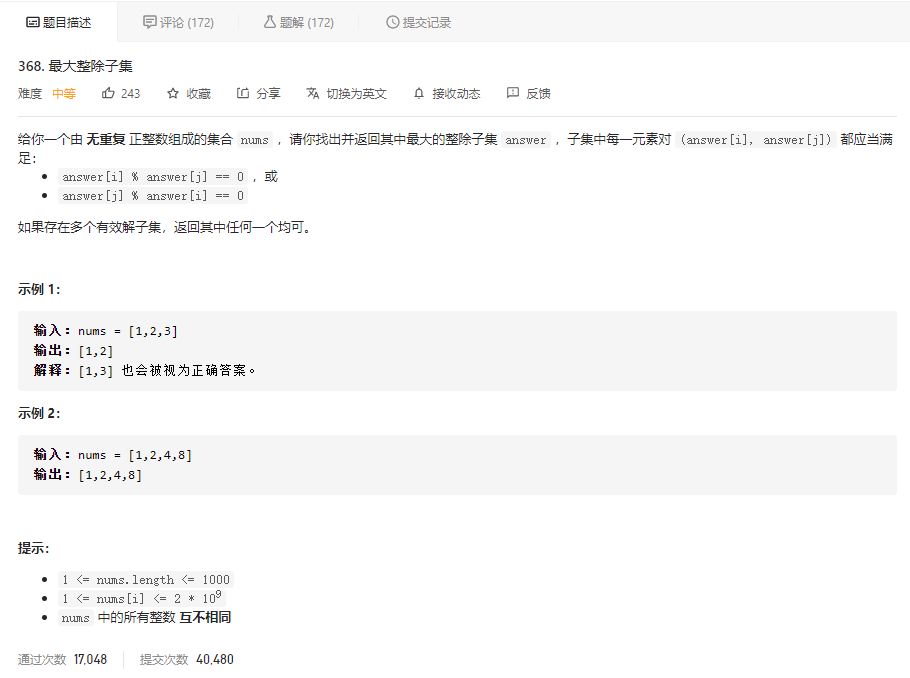
先看题目描述

cO2tbj.png

算法和思路

动态规划

  • 状态方程定义：dp[i] 表示以 nums[i] 为结尾的最大整除子集的大小，pre[i] 表示该最大整除子集中在其之前的元素的下标，若 pre[i] = -1 则表示 nums[i] 是该最大整除子集的第一个元素
  • 状态转移方程：对于所有小于 i 的 j，若 nums[i] % nums[j] = 0 且 dp[j] + 1 > dp[i]，则更新 dp[i] = dp[j] + 1
  • 初始化时令 dp 的所有元素为 1，pre 的所有元素为 1

遍历数组 nums 并更新 dp 和 pre，遍历过程中使用变量 max 和 maxIndex 维护 dp 数组中的最大值和最大值所在下标，最后根据该最大值所在下标和 pre 数组，往前找到在最大整除子集中当前元素的前一个元素，并添加到结果列表的首位，直至全部添加完，返回结果数组

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public List<Integer> largestDivisibleSubset(int[] nums) {
        Arrays.sort(nums);
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp, 1);
        int[] pre = new int[n];
        Arrays.fill(pre, -1);
        int max = 1;
        int maxIndex = 0;
        for (int i = 1; i < n; i++) {
            int num = nums[i];
            for (int j = i - 1; j >= 0; j--) {
                if (num % nums[j] == 0 && dp[j] + 1 > dp[i]) {
                    dp[i] = dp[j] + 1;
                    pre[i] = j;
                    if (dp[i] > max) {
                        max = dp[i];
                        maxIndex = i;
                    }
                }
            }
        }
        List<Integer> ans = new ArrayList<>();
        for (int i = maxIndex; i != -1; i = pre[i]) {
            ans.add(0, nums[i]);
        }
        return ans;
    }
}