解码方法

发表于
本文字数： 2.4k 阅读时长 ≈ 2 分钟

LeetCode每日一题，91. 解码方法

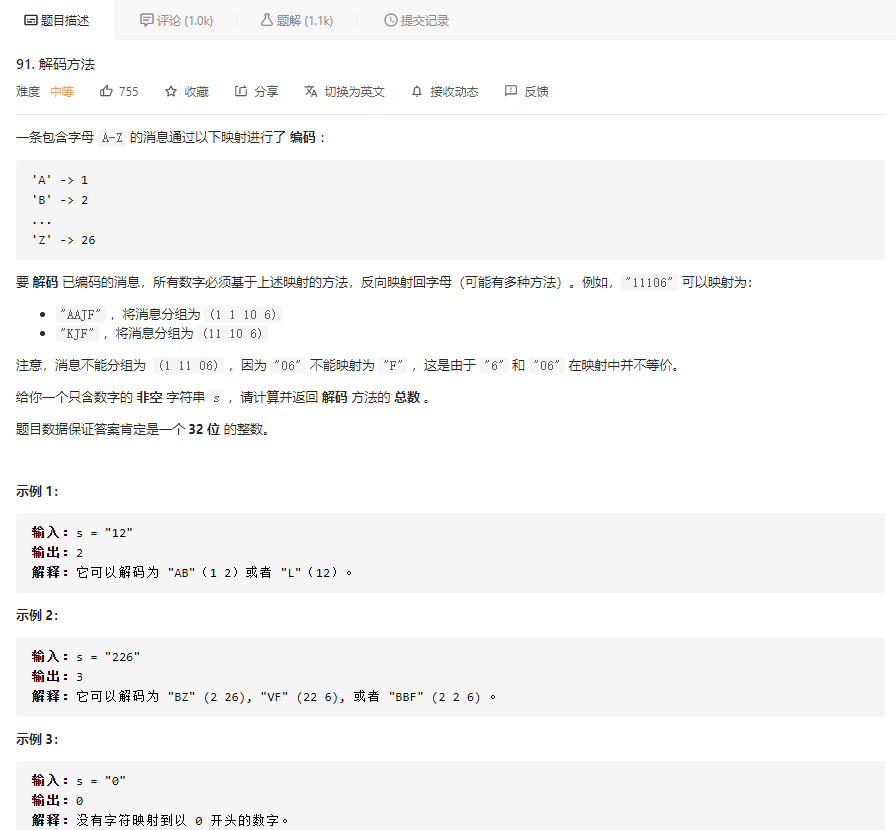
先看题目描述

cbw94s.png

算法和思路

动态规划

  • 状态方程：dp[i] 表示字符串 s[0：i - 1] 的解码方法总数，初始化 dp[0] = 1，表示空串有一种解码方法
  • 状态转移方程：dp[i] 由两部分组成，分别对应两种情况。一个是使用一个字符的情况，只要 s[i - 1] 不为 0，就可以用一个字符解码，dp[i] = dp[i - 1]；另一个是使用两个字符的情况，s[i - 2] 不为 0 且 s[i - 2] 和 s[i - 1] 组成的数字不超过 26，则可以使用两个字符解码，dp[i] = dp[i - 2]。将上面的两种状态转移方程在对应的条件满足时进行累加，就可得到 dp[i] 的值
  • 最后返回 dp[n] 即可

注意：由于上面的状态转移方程使用到了 dp[i - 2]，所以只有 i > 1 时才能进行转移。初始化边界条件 dp[0] = 1，若 s 的首字符不为 0 的话，dp[1] 也赋值为 1

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
 public int numDecodings(String s) {
        if (s.charAt(0) == '0') {
            return 0;
        }
        int n = s.length();
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        char[] cs = s.toCharArray();
        for (int i = 2; i <= n; i++) {
            int n2 = cs[i - 1] - '0';
            int n1 = cs[i - 2] - '0';
            if (n2 != 0) {
                dp[i] += dp[i - 1];
            }
            if (n1 != 0 && 10 * n1 + n2 <= 26) {
                dp[i] += dp[i - 2];
            }
        }
        return dp[n];
    }
}

可以看到状态转移方程中 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关，因此可以使用滚动数组的方法来优化空间复杂度，代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int numDecodings(String s) {
        if (s.charAt(0) == '0') {
            return 0;
        }
        int n = s.length();
        int a = 1;
        int b = 1;
        int c = 0;
        char[] cs = s.toCharArray();
        for (int i = 2; i <= n; i++) {
            int n2 = cs[i - 1] - '0';
            int n1 = cs[i - 2] - '0';
            if (n2 != 0) {
                c += b;
            }
            if (n1 != 0 && 10 * n1 + n2 <= 26) {
                c += a;
            }
            a = b;
            b = c;
            c = 0;
        }
        return b;
    }
}

下面是一开始使用的 dfs 算法的代码，结果跑超时了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    private int count = 0;

    public int numDecodings(String s) {
        dfs(s, 0);
        return count;
    }

    private void dfs(String s, int index) {
        if (index == s.length()) {
            count++;
            return;
        }
        if (s.charAt(index) == '0') {
            return;
        }
        dfs(s, index + 1);
        if (index < s.length() - 1 && Integer.valueOf(s.substring(index, index + 2)) <= 26) {
            dfs(s, index + 2);
        }
    }
}