打家劫舍II

发表于
本文字数： 2.2k 阅读时长 ≈ 2 分钟

LeetCode每日一题，213. 打家劫舍II

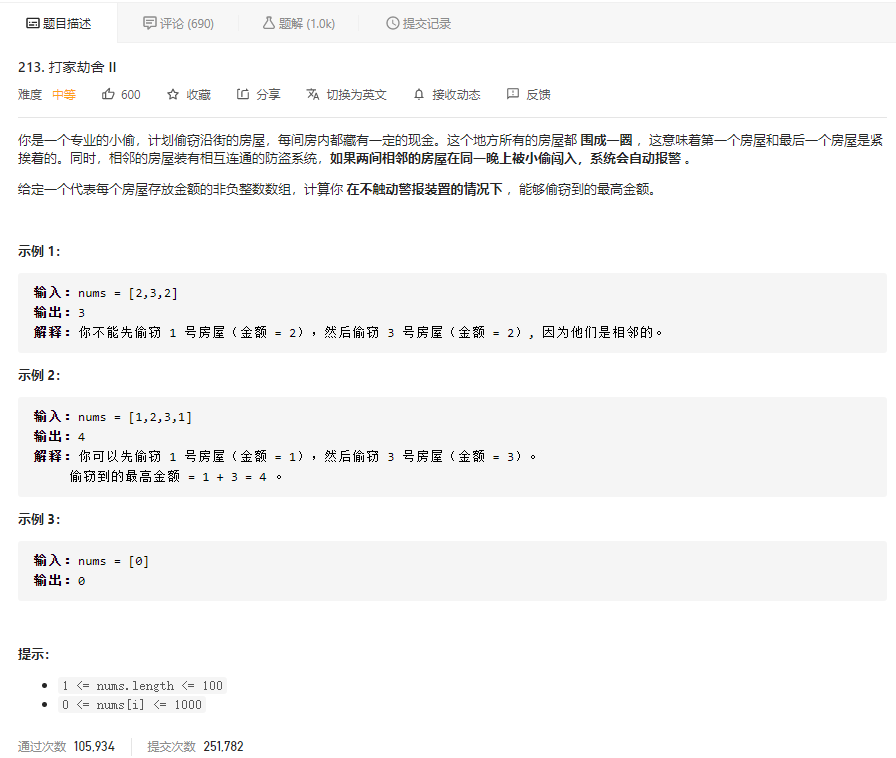
先看题目描述

c27stH.png

算法和思路

动态规划

  • 状态方程定义：设偷窃房屋的下标范围是 [start，end]，用 dp[i] 表示在下标范围 [start，i] 内可以偷窃到的最高总金额

  • 状态转移方程：dp[i] = max{dp[i - 2] + nums[i], dp[i - 1]}

  • 边界条件：dp[start] = nums[start]，dp[start + 1] = max{nums[start], nums[start + 1]}

分别取 (start，end) = (0，n - 2) 和 (start，end) = (1，n - 1) 进行计算，取两个 dp[end] 中的最大值，即可得到最终结果

由于 dp[i] 只与 dp[i - 1] 和 dp[i - 2] 有关，因此可以使用滚动数组优化

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        return Math.max(robRange(nums, 0, n - 2), robRange(nums, 1, n - 1));
    }

    public int robRange(int[] nums, int start, int end) {
        if (start == end) {
            return nums[start];
        }
        int first = nums[start];
        int second = Math.max(nums[start], nums[start + 1]);
        for (int i = start + 2; i <= end; i++) {
            int temp = second;
            second = Math.max(first + nums[i], second);
            first = temp;
        }
        return second;
    }
}

下面是自己一开始实现的代码，也是使用了动态规划，但是使用的状态方程不太一样，dp[i][0] 表示在 (0，i) 范围内不偷下标为 i 的房子情况下可盗窃的最大金额，dp[i][1] 表示在 (0，i) 范围内偷下标为 i 的房子情况下可盗窃的最大金额

状态转移方程为：dp[i][0] = max{dp[i - 1][1]，dp[i - 1][0]}，dp[i][1] = dp[i - 1][0] + nums[i]

然后分第一个房子偷不偷的两种情况进行考虑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public int rob(int[] nums) {
        int n = nums.length;
        if (n == 1) {
            return nums[0];
        }
        int ans = 0;
        int[][] dp = new int[n][2];
        for (int i = 0; i < 2; i++) {
            if (i == 0) {
                dp[0][1] = nums[0];
                dp[0][0] = Integer.MIN_VALUE;
            } else {
                dp[0][0] = 0;
                dp[0][1] = Integer.MIN_VALUE;
            }
            for (int j = 1; j < n; j++) {
                dp[j][0] = Math.max(dp[j - 1][0], dp[j - 1][1]);
                dp[j][1] = dp[j - 1][0] + nums[j];
            }
            if (i == 0) {
                ans = Math.max(ans, dp[n - 1][0]);
            } else {
                ans = Math.max(ans, Math.max(dp[n - 1][0], dp[n - 1][1]));
            }
        }
        return ans;
    }
}