LeetCode每日一题,264. 丑数 II
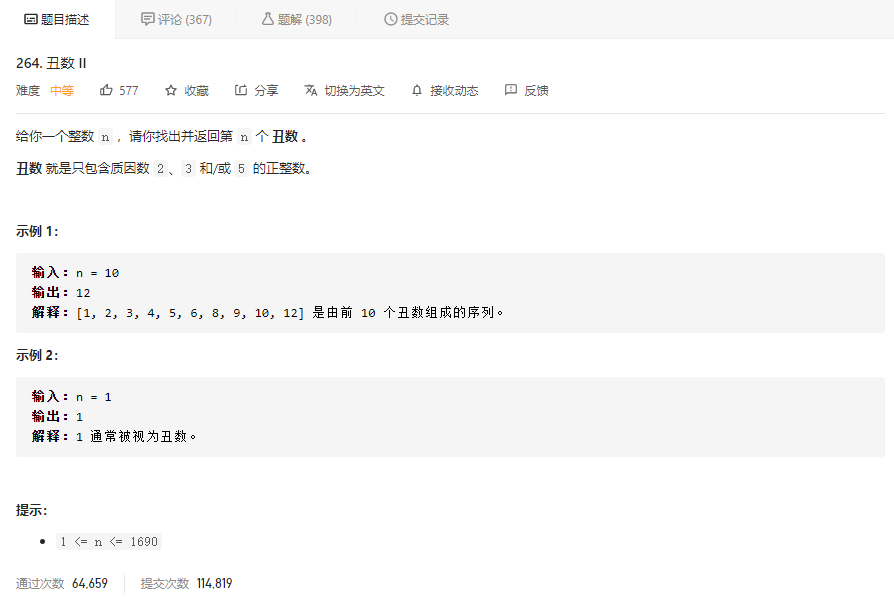
先看题目描述
算法和思路
最小堆
这题可使用最小堆实现,初始时堆为空,首先将最小的丑数 1 加入堆,每次取出堆顶元素 x,则 x 是堆中最小堆丑数,然后将 2x,3x,5x 也加入堆,为了避免重复元素的情况,可以使用有序集合实现这个最小堆,避免相同元素多次加入堆中,第 n 次从最小堆中取出的元素即为第 n 个丑数
动态规划
定义数组 dp,dp[i] 就表示第 i + 1 个丑数,初始化 dp[0] = 1
定义三个指针 p2,p3,p5,表示下一个丑数是当前指针指向的丑数乘以对应的质因数。初始时,三个指针都为 0
状态转移方程:dp[i] = min{dp[p2] * 2,dp[p3] * 3,dp[p5] * 5},然后分别比较 dp[i] 和 dp[p2] * 2,dp[p3] * 3,dp[p5] * 5 是否相等,若相等的话则将对应指针加 1
正确性说明:当 i > 0 时,对于 dp[i - 1],可以保证 dp[p2] * 2,dp[p3] * 3,dp[p5] * 5 均大于 dp[i - 1],而 dp[p2 - 1] * 2,dp[p3 - 1] * 3,dp[p5 - 1] * 5 均小于等于 dp[i - 1],因此 dp[i - 1] 之后的下一个丑数即 dp[i] 一定出现在 dp[p2] * 2,dp[p3] * 3,dp[p5] * 5 这三个数之中,取其中的最小值即可,然后将对应指针往后移 1 位
算法源码
最小堆
1 | class Solution { |
动态规划
1 | class Solution { |