LeetCode每日一题,1143. Longest Common Subsequence
先看题目描述
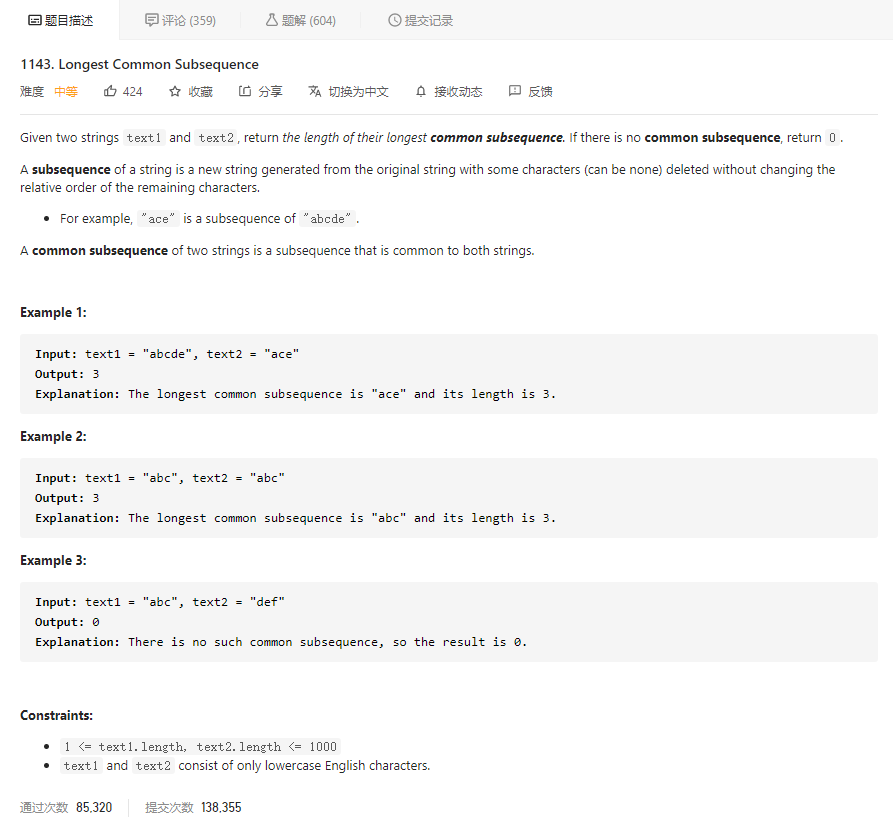
大意就是给定两个字符串 text1 和 text2,求其最长公共子序列长度
算法和思路
动态规划
这题挺简单的,只要想到了动态规划,构建二维的状态方程,一下就可以解决
- 状态方程:dp[i][j] 表示子串 text1[0:i - 1] 和子串 text2[0:j - 1] 的最长公共子序列长度
- 状态转移方程:
- 若 text1[i - 1] 和 text2[j - 1] 相等,则 dp[i][j] = dp[i - 1][j - 1] + 1
- 否则,dp[i][j] = max{dp[i - 1][j],dp[i][j - 1]}
设 text1 长度为 m,text2 长度为 n,最后返回 dp[m][n] 即可
算法源码
动态规划
1 | class Solution { |