132模式

LeetCode 每日一题，452. 132 Pattern

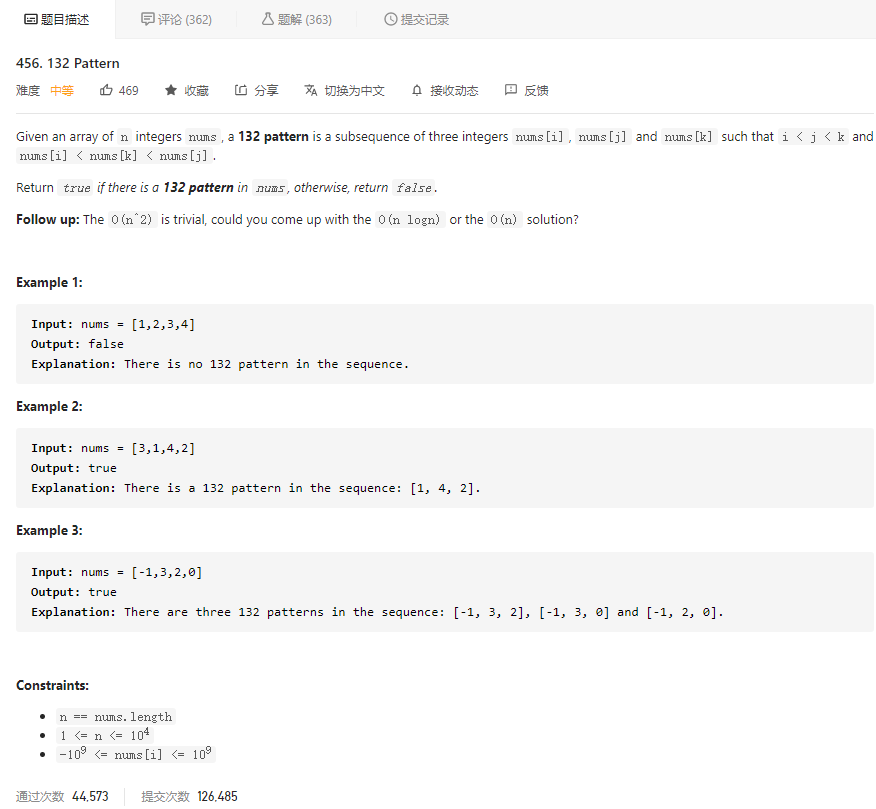
先看题目描述

大意就是给定一个数组 nums，问其中是否存在 132 模式的子序列，即是否存在 nums[i]，nums[j]，nums[k] 满足 i < j < k 且 nums[i] < nums[k] < nums[j]

算法和思路

枚举 3

我们从左到右枚举 3 的下标 j

由于 1 是模式中最小值，于是我们用一个变量 min 存储 nums[j] 左侧元素的最小值，当 min 大于等于 nums[j] 时，不可能以 j 作为 3 的下标构成 132 模式，直接去枚举下一个 j；否则，再去判断 nums[j] 右侧是否存在可以作为 2 的元素
为了快速的判断 nums[j] 右侧是否存在可以作为 2 的元素，我们可以将 nums[j] 右侧的元素存入一个 treeMap 中，以元素的值作为 key，出现次数作为 value，利用 treeMap 的键有序的特性，找出 nums[j] 右侧中大于 min 的最小元素，若该元素小于 nums[j]，则构成 132 模式，返回 true 即可；否则继续枚举

若枚举完后也没找到满足 132 模式的子序列，则返回 false

枚举 1

这题可以考虑从右到左进行枚举，用一个单调递减栈维护存储的元素，每当遍历到一个元素，将其入栈时，则将栈顶比它小的元素均弹出，并用一个变量 max 维护弹出元素的最大值，max 维护的实际上就是可以真正作为 2 的元素的最大值，因为遍历到 nums[i] 时，由于 max 维护的是被弹出元素的最大值，那么说明在 nums[i] 和 max 之间必定存在一个大于 max 的元素，此时只要判断 nums[i] 是否小于 max 即可，若小于 max，则可以构成 132 模式

具体到实现上

用单调栈维护所有可以作为 2 的候选元素，初始时，栈中只有 nums[len - 1]，使用变量 max 维护可以真正作为 2 的元素的最大值，初始时 max 的值为负无穷
然后从 len - 2 开始从右到左枚举元素 a[i]：
- 首先判断 nums[i] 是否可以作为 1，若 nums[i] < max，那么就说明找到了 132 模式
- 然后判断 nums[i] 是否可以作为 3，以此找出可以真正作为 2 的元素，将栈顶元素不断弹出直至栈顶元素大于等于 nums[i]，将栈顶元素弹出的同时要更新 max 的值
- 最后将 nums[i] 作为 2 的候选元素放入单调栈中
若最后也没找到满足 132 模式的子序列，返回 false

其实上面可以进行优化，若 nums[i] 与 max 相等，那么就没有必要将其与栈顶元素比较了，因为这样无论是它弹出的栈顶元素，还是未来它自己被弹出时，都不可能更新 max 的值

算法源码

枚举 3

class Solution {
    public boolean find132pattern(int[] nums) {
        int len = nums.length;
        int min = nums[0];
        TreeMap<Integer, Integer> treeMap = new TreeMap<>();
        for (int i = 2; i < len; i++) {
            int num = nums[i];
            treeMap.put(num, treeMap.getOrDefault(num, 0) + 1);
        }
        for (int i = 1; i < len - 1; i++) {
            int num = nums[i];
            if (min < num) {
                Integer next = treeMap.higherKey(min);
                if (next != null && next < num) {
                    return true;
                }
            }
            min = Math.min(min, num);
            int cnt = treeMap.get(nums[i + 1]);
            if (cnt == 1) {
                treeMap.remove(nums[i + 1]);
            } else {
                treeMap.put(nums[i + 1], cnt - 1);
            }
        }
        return false;
    }
}

枚举 1

class Solution {
    public boolean find132pattern(int[] nums) {
        int len = nums.length;
        int max = Integer.MIN_VALUE;
        Deque<Integer> stack = new ArrayDeque<>();
        stack.push(nums[len - 1]);
        for (int i = len - 2; i >= 0; i--) {
            if (nums[i] < max) {
                return true;
            }
            if (nums[i] > max) {
                while (!stack.isEmpty() && nums[i] > stack.peek()) {
                    max = Math.max(max, stack.pop());
                }
                stack.push(nums[i]);
            }
        }
        return false;
    }
}

使用整型数组和一个代表栈顶的 top 指针来代替栈的使用，能进一步提高运行速度

class Solution {
    public boolean find132pattern(int[] nums) {
        int len = nums.length;
        int max = Integer.MIN_VALUE;
        int top = 0;
        int[] stack = new int[len];
        stack[0] = nums[len - 1];
        for (int i = len - 2; i >= 0; i--) {
            int num = nums[i];
            if (num < max) {
                return true;
            }
            if (num > max) {
                while (top >= 0 && num > stack[top]) {
                    max = Math.max(max, stack[top]);
                    top--;
                }
                stack[++top] = num;
            }
        }
        return false;
    }
}