LeetCode每日一题,73. Set Matrix Zeros
先看题目描述
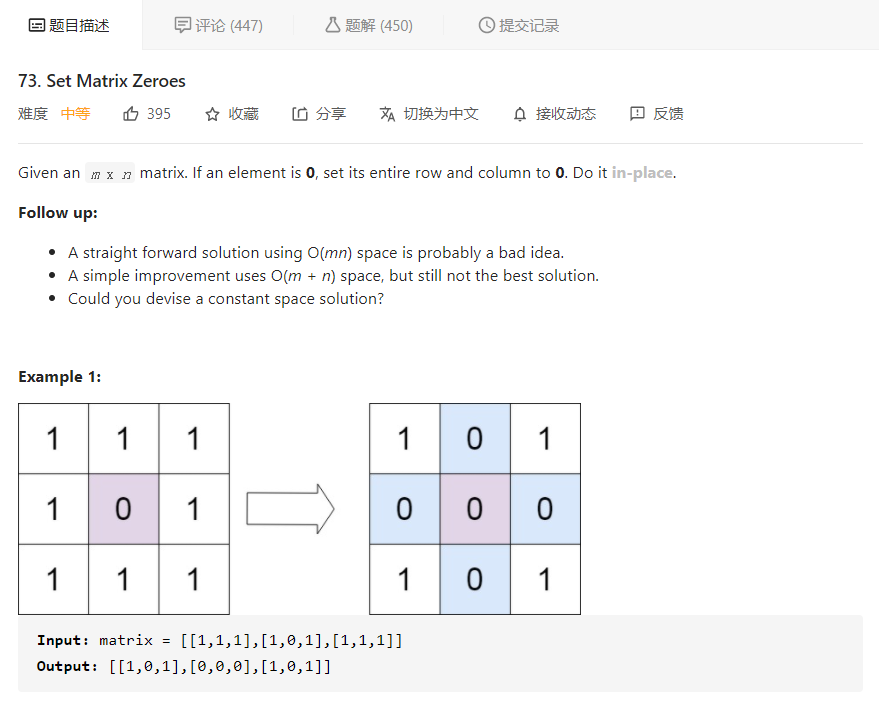
大意就是给定一个矩阵,若矩阵中某个元素为 0,则将该行和该列的所有元素都置为 0
算法和思路
标记数组
这是 O(m + n) 的空间复杂度的解法,思路就是使用两个布尔数组 rows 和 cols,记录某行或某列是否需要翻转。遍历数组 matrix 的所有元素,遍历到 matrix[i][j] 时,若值为 0,则令 rows[i] 为 true,cols[j] 为 true,遍历完 matrix 后,再去遍历 rows 和 cols 数组,若值为 true,则将相应行或相应列全置 0
算法源码
标记数组
1 | class Solution { |
使用两个标记变量
这是空间复杂度为 O(1) 的解法,思路就是使用两个标记变量分别记录第 0 行和第 0 列是否包含 0。遍历除了第 0 行和第 0 列外的其他所有元素,遍历到 matrix[i][j] 时,若值为 0,则令 matrix[i][0] 和 matrix[0][j] 为 0,代表第 i 行和第 i 列均需要被置 0。然后遍历第 0 行和第 0 列的元素,遍历到值为 0 的元素时则将对应行或列置 0,最后通过两个标记变量将第 0 行或第 0 列置 0
1 | class Solution { |