不同的子序列

发表于
本文字数： 1.6k 阅读时长 ≈ 1 分钟

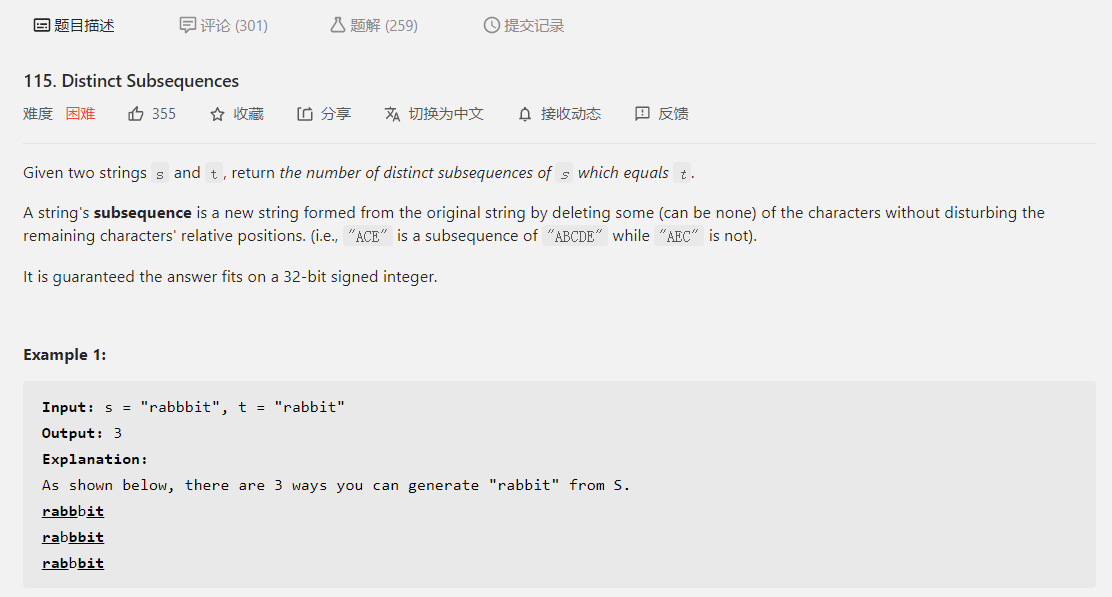
LeetCode题目，115. Distinct Subsequences

先看题目描述

66u0vd.png

大意就是给定一个字符串 s 和字符串 t，让我们计算 s 中与 t 相等的子序列个数并返回

算法和思路

动态规划

这题看着比较难，但其实只要想到可以用动态规划解决，想明白状态转移方程和边界条件，这道题就很好解决

设字符串 s 的长度为 n，字符串 t 的长度为 m，构建一个长度为 m + 1，宽度为 n + 1 的二维数组 dp

  • 状态方程定义：dp[i][j] 表示字符串 s[0：j - 1] 中与 t[0：i - 1] 相等的子序列的数量
  • 状态转移方程：
    • 若 t[i - 1] 与 s[j - 1] 相等，则 dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1]
    • 否则，dp[i][j] = dp[i][j - 1]

为了方便状态转移，初始化时将 dp[0] 的所有元素都置为 1，最后返回 dp[m][n] 即可

关于对状态转移方程的理解：当 t[i - 1] 与 s[j - 1] 不相等时，t[i - 1] 与 s[j - 1] 不匹配，因此只考虑 t[0：i - 1] 作为 s[0：j - 2] 的子序列，因此有 dp[i][j] = dp[i][j - 1]；当 t[i - 1] 与 s[j - 1] 相等时，此时有两种选择，一种是 t[i - 1] 与 s[j - 1] 不匹配，这部分对 dp[i][j] 的贡献是 dp[i][j - 1]，另一种是 t[i - 1] 与 s[j - 1] 匹配，此时要考虑 t[0：i - 2] 作为 s[0：j - 2] 的子序列，这部分对 dp[i][j] 的贡献是 dp[i - 1][j - 1]，因此有 dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1]

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int numDistinct(String s, String t) {
        int m = t.length();
        int n = s.length();
        if (m > n) {
            return 0;
        }
        if (s.equals(t)) {
            return 1;
        }
        char[] cs = s.toCharArray();
        char[] ct = t.toCharArray();
        int[][] dp = new int[m + 1][n + 1];
        Arrays.fill(dp[0], 1);
        for (int i = 1; i <= m; i++) {
            for (int j = i; j <= n; j++) {
                if (ct[i - 1] == cs[j - 1]) {
                    dp[i][j] = dp[i][j - 1] + dp[i - 1][j - 1];
                } else {
                    dp[i][j] = dp[i][j - 1];
                }
            }
        }
        return dp[m][n];
    }
}