验证二叉树的前序序列化

发表于
本文字数： 4.7k 阅读时长 ≈ 4 分钟

LeetCode每日一题，331. Verify Preorder Serialization of a Binary Tree

先看题目描述

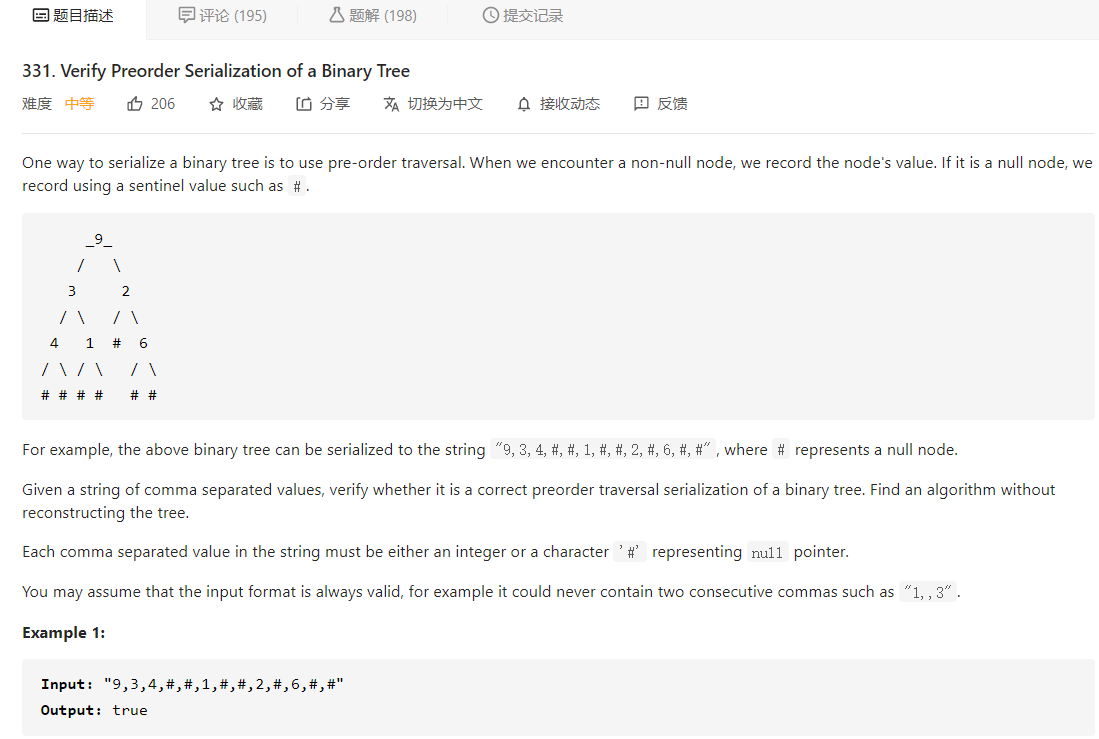
6UCuy6.png

大意就是给定一个字符串表示的二叉树的前序遍历序列，其中数字代表非叶子节点，# 代表叶子节点，节点间通过逗号隔开，让我们通过前序遍历序列判断该二叉树是否是个完整的二叉树(即每个非叶子节点是否都有两个子节点)

算法和思路

栈

可以引入一个概念，叫做槽位，一个槽位可以看作是当前二叉树中正在等待被节点填充的位置

我们定义一个栈，初始时，栈中只有 1，栈顶元素对应着下一步可用的槽位数量，当遇到 # 即叶子节点时，则填充一个槽位，将栈顶元素减 1；当遇到数字即非叶子节点时，则将栈顶元素减 1，并将 2 添加至栈顶，代表填充一个槽位，同时引入两个新槽位。注意，当栈顶元素变为 0 时，就将该元素移除。最后检查栈是否为空即可，同时，在填充槽位的过程中，若槽位数量不足，同样是非法序列

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public boolean isValidSerialization(String preorder) {
        int len = preorder.length();
        char[] cs = preorder.toCharArray();
        int index = 0;
        Deque<Integer> stack = new ArrayDeque<>();
        stack.push(1);
        while (index < len) {
            char c = cs[index];
            if (c == ',') {
                index++;
            } else if (c == '#') {
                if (stack.isEmpty()) {
                    return false;
                }
                int top = stack.pop();
                top--;
                if (top > 0) {
                    stack.push(top);
                }
                index++;
            } else {
                if (stack.isEmpty()) {
                    return false;
                }
                while (index < len && Character.isDigit(cs[index])) {
                    index++;
                }
                int top = stack.pop();
                top--;
                if (top > 0) {
                    stack.push(top);
                }
                stack.push(2);
            }
        }
        return stack.isEmpty();
    }
}

也可以把栈中元素看作一个整体，即用一个计数器维护所有的剩余槽位数量，初始时计数器的值为 1，当遇到 # 时将计数器减 1，代表消耗一个槽位；遇到数字时将计数器加 1，代表所有的剩余槽位数量增加了一个。过程中若出现槽位数量不够的情况就代表是个非法序列，最后判断计数器的值是否为 0 即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public boolean isValidSerialization(String preorder) {
        int len = preorder.length();
        char[] cs = preorder.toCharArray();
        int index = 0;
        int slots = 1;
        while (index < len) {
            if (slots == 0) {
                return false;
            }
            char c = cs[index];
            if (c == ',') {
                index++;
            } else if (c == '#') {
                slots--;
                index++;
            } else {
                while (index < len && Character.isDigit(cs[index])) {
                    index++;
                }
                slots++;
            }
        }
        return slots == 0;
    }
}

下面是自己一开始实现的算法，也是使用的栈，但是引入了一个表示节点的数据结构，实现的没上面方法巧妙，运行速度较慢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    public boolean isValidSerialization(String preorder) {
        if (preorder.equals("#")) {
            return true;
        }
        String[] vals = preorder.split(",");
        Deque<Node> stack = new ArrayDeque<>();
        for (int i = 0; i < vals.length; i++) {
            String s = vals[i];
            if (s.equals("#")) {
                if (stack.isEmpty()) {
                    return false;
                } else {
                    while (!stack.isEmpty()) {
                        Node fa = stack.peek();
                        if (fa.isHasLeft()) {
                            stack.pop();
                        } else {
                            fa.setHasLeft(true);
                            break;
                        }
                    }
                } 
            } else {
                if (stack.isEmpty() && i != 0) {
                    return false;
                }
                stack.push(new Node(Integer.valueOf(s)));
            }
        }
        return stack.isEmpty();
    }

    private class Node {
        private int val;
        private boolean hasLeft;
        private boolean hasRight;

        public Node(int val) {
            this.val = val;
            this.hasLeft = false;
            this.hasRight = false;
        }

        public void setHasLeft(boolean hasLeft) {
            this.hasLeft = hasLeft;
        }

        public boolean isHasLeft() {
            return hasLeft;
        }

        public void setHasRight(boolean hasRight) {
            this.hasRight = hasRight;
        }

        public boolean isHasRight() {
            return hasRight;
        }
    }
}

其实上面的办法，总结下来，就是利用了完整二叉树的性质，即叶子节点的数目等于非叶子节点的数目 + 1

证明如下：设非叶子节点的数目为 m，叶子节点的数目为 n。由于非叶子节点的出度为 2，叶子节点的出度为 0，那么二叉树中边的数目为 2m，根据五环连通图的性质有 节点个数 = 边的个数 + 1，即节点个数为 2m + 1；又因为节点只包括非叶子节点和叶子节点，于是有节点个数 = m + n，故 m + n = 2m + 1，可得 n = m + 1