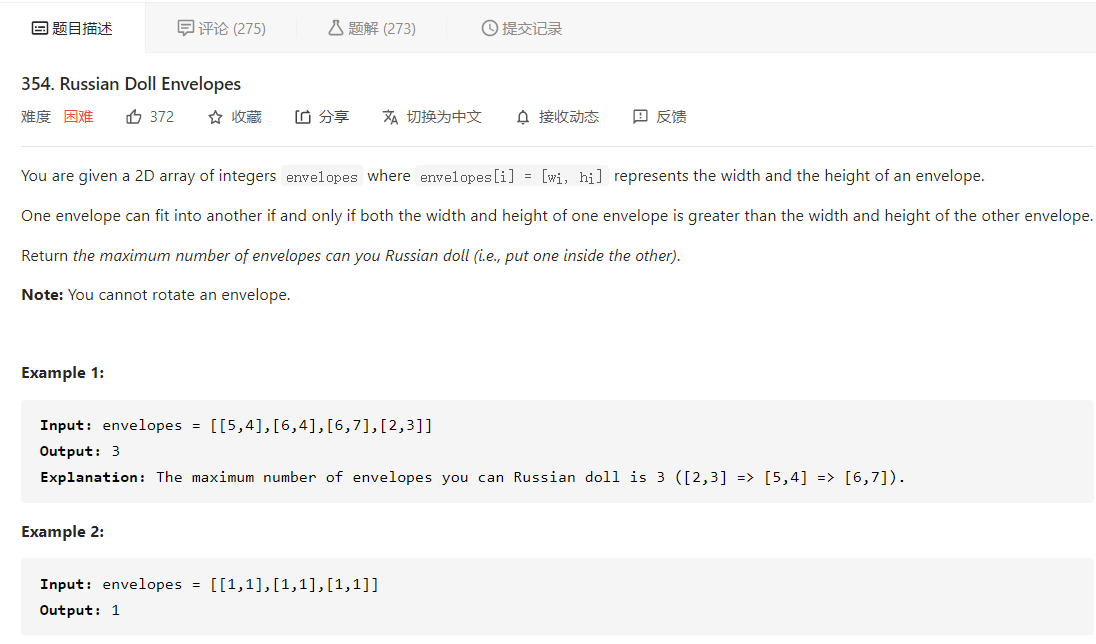
LeetCode每日一题,354. Russian Doll Envelopes
先看题目描述
大意就是给定一个数组 envelopes 存储多个信封的宽度和长度,一个信封可以被套进另一个信封当且仅当它的宽度和长度都小于另一个信封,问最多有多少个信封能像俄罗斯套娃一样套起来
算法和思路
动态规划——01背包
一开始看到这题,是想到用类似01背包问题的思路来动态规划,状态方程 d[i][j][k] 代表从第 k 个信封开始,只能被套在宽度大于 i 且长度大于 j 的信封的情况下的最大数量设第 k 个信封的宽度为 w,高度为 h
若 w 大于 i 且 h 大于 j,状态转移方程就为 d[i][j][k] = max{d[i][j][k + 1],d[w][h][k + 1] + 1}
否则,状态转移方程为 d[i][j][k] = d[i][j][k + 1]
最后的结果为 d[0][0][0]
动态规划——最长递增子序列
上面这个方法跑超时了,就去看题解,发现应该用最长递增子序列的思路
最长子序列问题:给定一个序列,我们需要找出一个最长的子序列,使得这个子序列中的所有元素严格单调递增
我们可以对信封序列按照宽度升序排列,当宽度相同时按照高度降序排列(这样可以保证对于相同的 w 值,其对应的 h 值不可能组成长度超过 1 的严格递增序列),这样问题就转化为了对于信封的 h 维度,找出 h 维度的最长严格递增子序列,其长度即为答案
接着解决最长递增子序列问题即可,下面给出两种解决最长递增子序列问题的代码
动态规划:状态方程 dp[i] 表示以第 i 个数字为结尾的最长递增子序列长度(nums[i] 必须被选取),转移方程为 dp[i] = max{dp[j]} + 1,其中 j 满足 0 <= j < i 且 nums[j] < nums[i]
1 | class Solution { |
贪心 + 二分查找:维护一个数组 d[i],表示长度为 i 的最长递增子序列的末尾元素的最小值,用 len 记录目前最长递增子序列的长度,起始时 len = 1,d[1] = nums[0]。可以用反证法证明数组 d 是单调递增的,即数组 d 有序,于是就可以使用二分查找,最后返回长度 len 即可
整个算法流程为:
- 设当前已求出的最长上升子序列的长度为 len(初始时为 1),从前往后遍历数组 nums,在遍历到 nums[i] 时:
- 若 nums[i] > d[len],则直接加入到 d 数组末尾,并更新 len = len + 1
- 否则,在 d 数组中二分查找,找到第一个比 nums[i] 小的数 d[k],并更新 d[k + 1] = nums[i]
1 | class Solution { |
算法源码
动态规划——01背包
这个代码跑超时了
1 | class Solution { |
动态规划——最长递增子序列
1 | class Solution { |