比特位计数

发表于
本文字数： 2.1k 阅读时长 ≈ 2 分钟

LeetCode每日一题，338. Count Bits

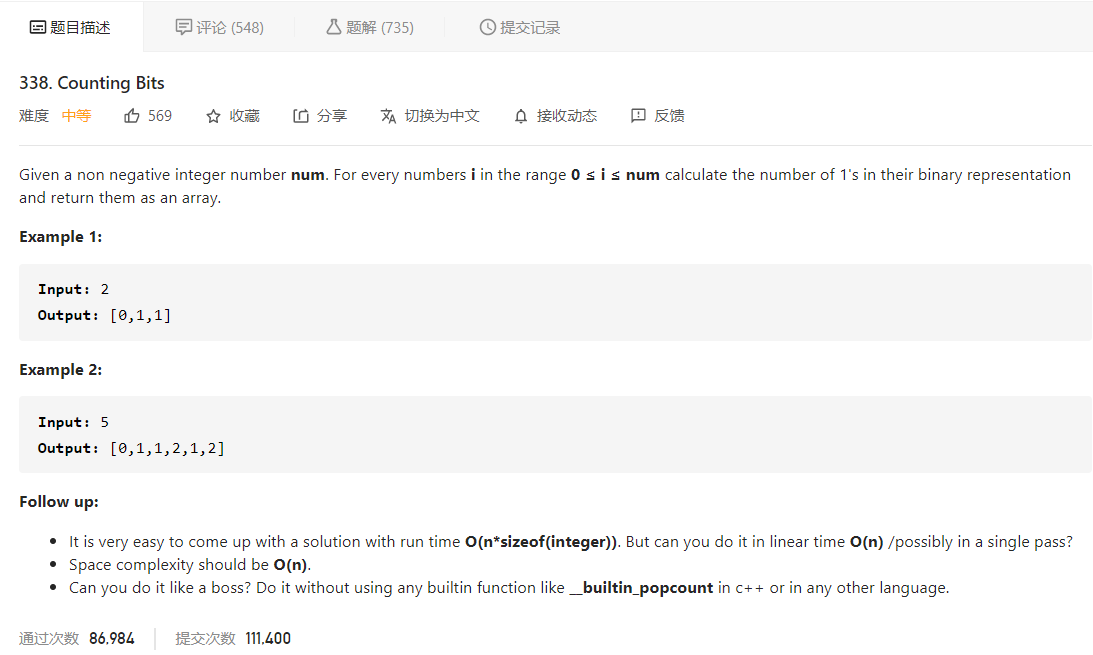
先看题目描述

6AMwut.png

大致意思就是给定一个数字 num，让我们对于 0 至 num 之间的所有数，计算其二进制表示下 1 的个数，并以数组形式返回

算法和思路

动态规划

思路就是对于每个数 i，若 i 是 2 的整数幂，则其二进制表示下 1 的个数就等于 1；否则，设小于 i 的最大的 2 的整数幂为 pre，i 的二进制表示下 1 的个数就为 ans[i] = ans[i - pre] + 1

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int[] countBits(int num) {
        int[] ans = new int[num + 1];
        int pre = 1;
        for (int i = 1; i <= num; i++) {
            if (i == pre * 2) {
                ans[i] = 1;
                pre = i;
            } else {
                ans[i] = 1 + ans[i - pre];
            }
        }
        return ans;
    }
}

做完以后去看题解，才发现这道题有很多种动态规划的方法，也有直接计算的方法

直接计算

按位与计算的一个性质是：对于任意整数，令 x = x & (x - 1)，该运算会将 x 的二进制表示下的最后一个 1 变成 0.因此，对 x 重复该操作，直至 x 变为 0，则操作次数即为 x 的一比特数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 0; i <= num; i++) {
            bits[i] = countOnes(i);
        }
        return bits;
    }

    public int countOnes(int x) {
        int ones = 0;
        while (x > 0) {
            x &= (x - 1);
            ones++;
        }
        return ones;
    }
}

动态规划——最高有效位

这个方法实际上就是我自己想出来的那个方法，思路基本一致

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        int highBit = 0;
        for (int i = 1; i <= num; i++) {
            if ((i & (i - 1)) == 0) {
                highBit = i;
            }
            bits[i] = bits[i - highBit] + 1;
        }
        return bits;
    }
}

动态规划——最低有效位

1
2
3
4
5
6
7
8
9
class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            bits[i] = bits[i >> 1] + (i & 1);
        }
        return bits;
    }
}

动态规划——最低设置位

1
2
3
4
5
6
7
8
9
class Solution {
    public int[] countBits(int num) {
        int[] bits = new int[num + 1];
        for (int i = 1; i <= num; i++) {
            bits[i] = bits[i & (i - 1)] + 1;
        }
        return bits;
    }
}