二维区域和检索

发表于
本文字数： 2.2k 阅读时长 ≈ 2 分钟

LeetCode每日一题，304. Range Sum Query 2D - Immutable

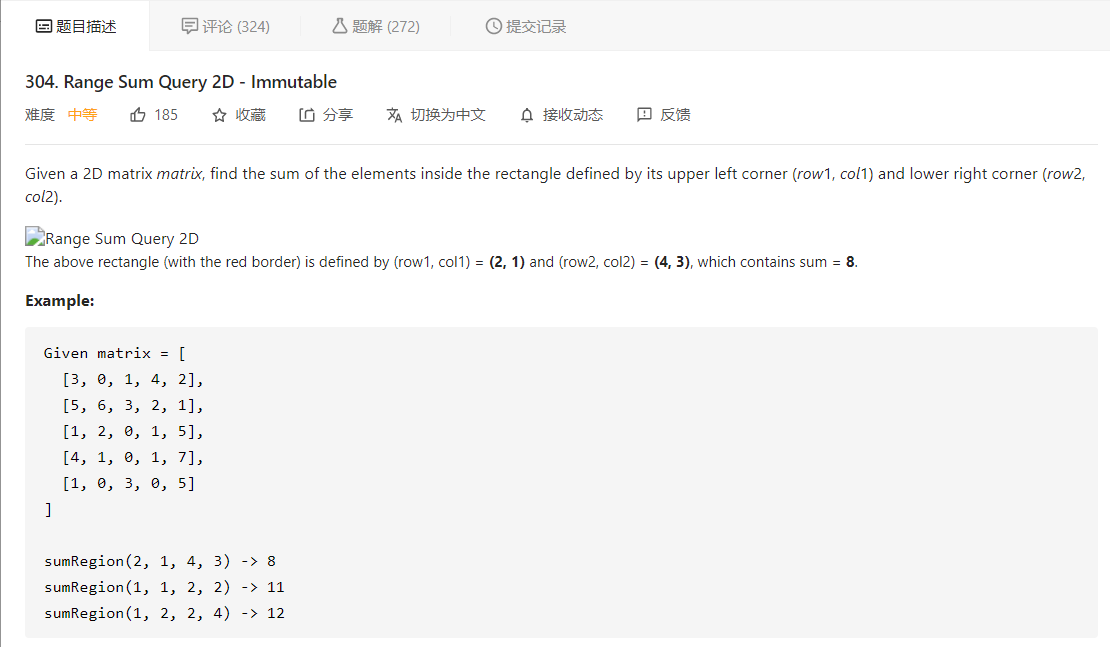
先看题目描述

6FUjHA.png

大意就是给定一个二维矩阵，让我们实现一个类，给定子矩阵的左上角 (row1，col1) 和右下角 (row2，col2)，让我们求出该子矩阵内的元素之和

算法和思路

一维前缀和

设矩阵的行数为 m，列数为 n，初始化时把二维矩阵看作 m 个一维数组，对每一行计算前缀和即可。创建一个 m 行 n + 1 列的二维数组 prefix，prefix[i] 为 matrix[i] 的前缀和数组。检索时对子矩阵的每一行计算子数组和，最后将结果累加返回即可

二位前缀和

上面的方法虽然可以做出来，但每一次检索时都要遍历多个前缀和数组，不能达到 O(1) 的时间复杂度，使用二维前缀和的方法可以优化达到 O(1) 时间复杂度的检索

设矩阵的行数为 m，列数为 n，创建一个 m + 1 行 n + 1 列的二维数组 sum 用来存储该二维矩阵的前缀和。sum[i][j] 表示以 (0，0) 为左上角，(i - 1，j - 1) 为右下角的子矩阵的元素之和，sum 数组的第一行和第一列没有实际意义，只是为了方便计算使用，第一行和第一列的所有元素均为 0。sum[i][j] 的推导公式为 sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1]

检索时我们通过 sum 数组来求即可，给定子矩阵的左上角 (row1，col1) 和右下角 (row2，col2)，该子矩阵的元素之和为：sum[row2 + 1][col2 + 1] - sum[row1][col2 + 1] - sum[row2 + 1][col1] + sum[row1][col1]

算法源码

一维前缀和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class NumMatrix {
    private int[][] prefix;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m == 0) {
            return;
        }
        int n = matrix[0].length;
        this.prefix = new int[m][n + 1];
        for (int i = 0; i <m; i++) {
            for (int j = 0; j <n; j++) {
                prefix[i][j + 1] = prefix[i][j] + matrix[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int sum = 0;
        for (int i = row1; i <= row2; i++) {
            sum += prefix[i][col2 + 1] - prefix[i][col1];
        }
        return sum;
    }
}

二维前缀和

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class NumMatrix {
    private int[][] sum;

    public NumMatrix(int[][] matrix) {
        int m = matrix.length;
        if (m > 0) {
            int n = matrix[0].length;
            this.sum = new int[m + 1][n + 1];
            for (int i = 1; i <= m; i++) {
                for (int j = 1; j <= n; j++) {
                    sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
                }
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2 + 1][col2 + 1] - sum[row1][col2 + 1] - sum[row2 + 1][col1] + sum[row1][col1];
    }
}