连续子数组的最大和

发表于
本文字数： 994 阅读时长 ≈ 1 分钟

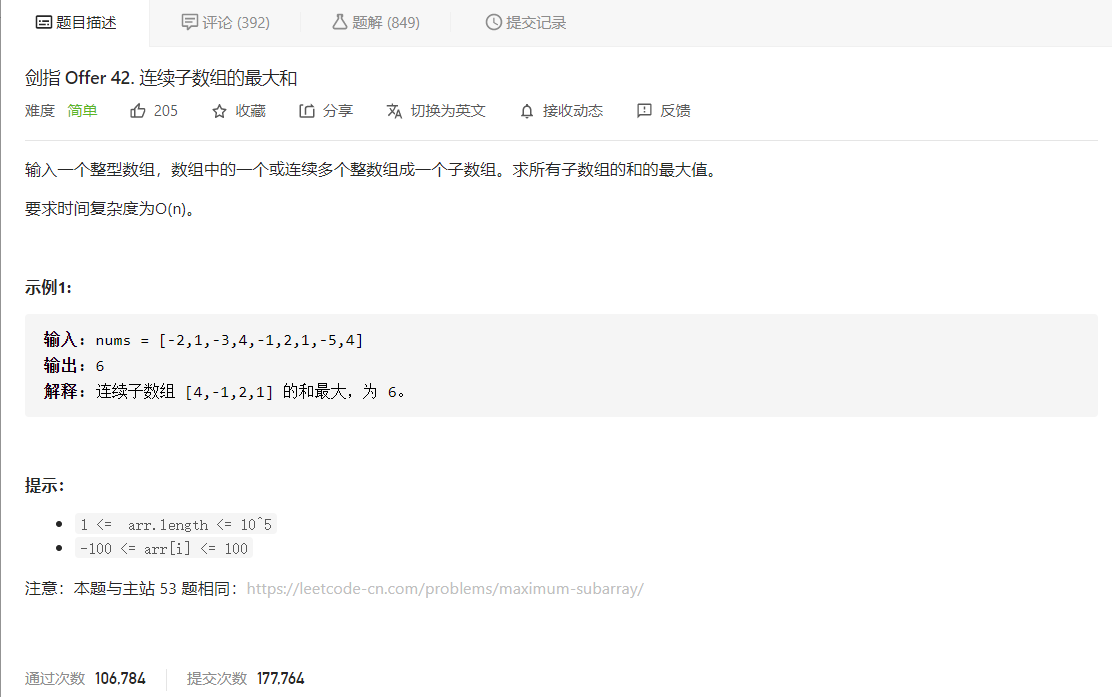
LeetCode题目，剑指 Offer 42. 连续子数组的最大和

先看题目描述

6S5MVS.png

算法和思路

动态规划

这题我们可以使用动态规划解决

  • 定义状态方程 dp[i] 表示以 nums[i] 结尾的子数组的最大值
  • 状态转移方程为：dp[i] = nums[i] + max{0，dp[i - 1]}；因为若 dp[i - 1] < 0，说明其对 dp[i] 有负贡献，不如舍去
  • 初始状态为 dp[0] = nums[0]
  • 最后返回 dp 列表中的最大值即可

算法源码

动态规划

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int[] dp = new int[len];
        int res = nums[0];
        dp[0] = nums[0];
        for (int i = 1; i < len; i++) {
            dp[i] = nums[i] + Math.max(dp[i - 1], 0);
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

由于状态转移方程中 dp[i] 只与 dp[i - 1] 有关，因此可以使用滚动数组的思路优化空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int maxSubArray(int[] nums) {
        int len = nums.length;
        int res = nums[0];
        int num = nums[0];
        for (int i = 1; i < len; i++) {
            num = nums[i] + Math.max(0, num);
            res = Math.max(res, num);
        }
        return res;
    }
}