K连续位的最小翻转次数

发表于
本文字数： 1.2k 阅读时长 ≈ 1 分钟

LeetCode每日一题，995. Minimum Number of K Consecutive Bit Flips

先看题目描述

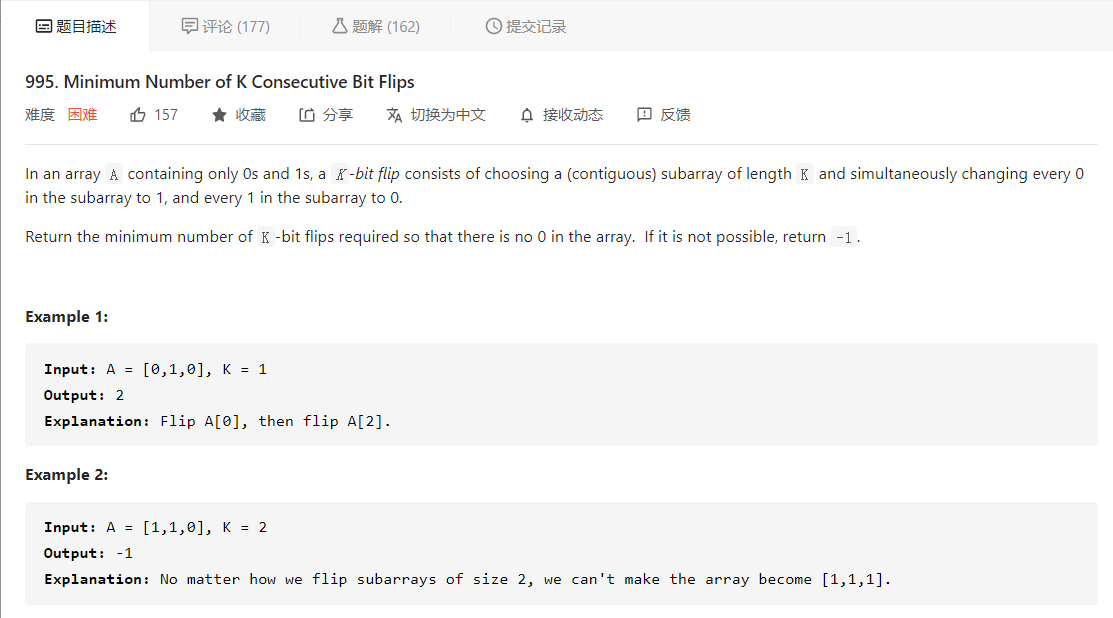
yWwneg.png

大意就是给定一个数组 A 和 数字 K，A 中只含 0 和 1，我们每次可以将 A 中连续的 K 位数字翻转，问最少翻转多少次，可以使 A 中的元素全为 1，若不能通过翻转使得 A 中元素全为 1，则返回 -1

算法和思路

这题想了好久，没想出来，就去看题解了

差分数组

我们用差分数组的思想来计算当前数字翻转的次数。我们可以维护一个差分数组 diff，其中 diff[i] 表示两个相邻元素 A[i] 和 A[i - 1] 的翻转次数之差，即 diff[i] = A[i] 的翻转次数 - A[i - 1] 的翻转次数，对于区间 [l，r]，将其翻转次数全部加 1，只会影响到 l 和 r + 1 处的差分值，故将 diff[l] 增加 1，diff[r + 1] 减少 1

通过累加差分数组可以得到当前位置的翻转次数，我们用一个变量 revCount 维护该累加值

遍历到 A[i] 时，若 A[i] + revCount 为偶数，则说明当前元素的实际值为 0，需要翻转区间 [i，i + K - 1]，我们可以直接将 revCount 加 1，diff[i] 增加 1，diff[i + K] 减少 1

需注意若 i + K > 数组 A 的长度，则剩余区间长度不够翻转，无法执行翻转操作，直接返回 -1

算法源码

差分数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minKBitFlips(int[] A, int K) {
        int n = A.length;
        int[] diff = new int[n + 1];
        int revCount = 0;
        int ans = 0;
        for (int i = 0; i < n; i++) {
            revCount += diff[i];
            if ((revCount + A[i]) % 2 == 0) {
                if ((i + K) > n) {
                    return -1;
                }
                ans++;
                revCount++;
                diff[i]++;
                diff[i + K]--;
            }
        }
        return ans;
    }
}