杨辉三角 II

发表于
本文字数： 1.9k 阅读时长 ≈ 2 分钟

LeetCode每日一题，119. Pascal’s Triangle II

先看题目描述

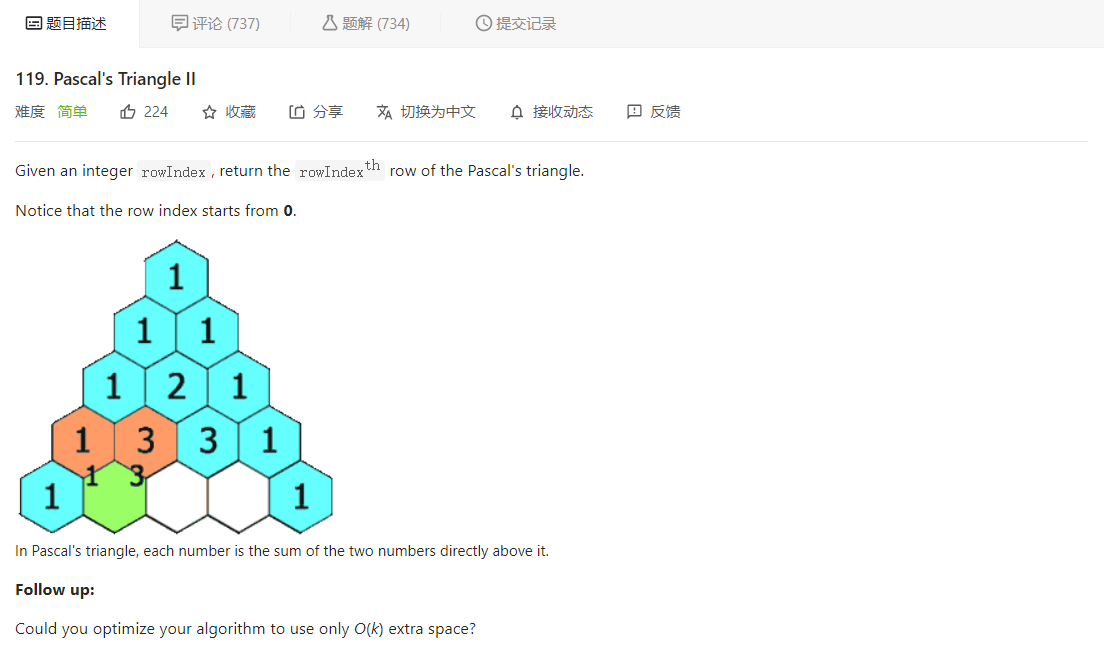
yDVQyt.png

大意就是给定一个整数 rowIndex，让我们返回杨辉三角的第 rowIndex 行

算法和思路

这题了解杨辉三角的性质就可以使用递推来解决，设第 rowIndex 行的长度为 len，其上一行为 pre，那么 rowIndex 的第 0 个和第 len - 1 个元素均为 1，而对于第 i 个元素(0 < i < len - 1)，rowIndex[i] = pre[i - 1] + pre[i]

算法源码

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> ans = new ArrayList<>();
        ans.add(1);
        if (rowIndex == 0) {
            return ans;
        }
        int len = rowIndex + 1;
        List<Integer> pre = getRow(rowIndex - 1);
        for (int i = 1; i < len - 1; i++) {
            ans.add(pre.get(i - 1) + pre.get(i));
        }
        ans.add(1);
        return ans;
    }
}

递推

下面是题解的使用滚动数组优化的递推方法的代码，由于对第 i+1 行的计算仅用到了第 i 行 的数据，因此可以使用滚动数组的思想优化空间复杂度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> pre = new ArrayList<Integer>();
        for (int i = 0; i <= rowIndex; ++i) {
            List<Integer> cur = new ArrayList<Integer>();
            for (int j = 0; j <= i; ++j) {
                if (j == 0 || j == i) {
                    cur.add(1);
                } else {
                    cur.add(pre.get(j - 1) + pre.get(j));
                }
            }
            pre = cur;
        }
        return pre;
    }
}

还可以进一步优化，只使用一个数组解决，当前行第 i 项的计算只与上一行第 i−1 项及第 i 项有关。因此我们可以倒着计算当前行，这样计算到第 i 项时，第 i−1 项仍然是上一行的值，下面是代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public List<Integer> getRow(int rowIndex) {
        List<Integer> row = new ArrayList<Integer>();
        row.add(1);
        for (int i = 1; i <= rowIndex; ++i) {
            row.add(0);
            for (int j = i; j > 0; --j) {
                row.set(j, row.get(j) + row.get(j - 1));
            }
        }
        return row;
    }
}