K个不同整数的子数组

发表于
本文字数： 2.4k 阅读时长 ≈ 2 分钟

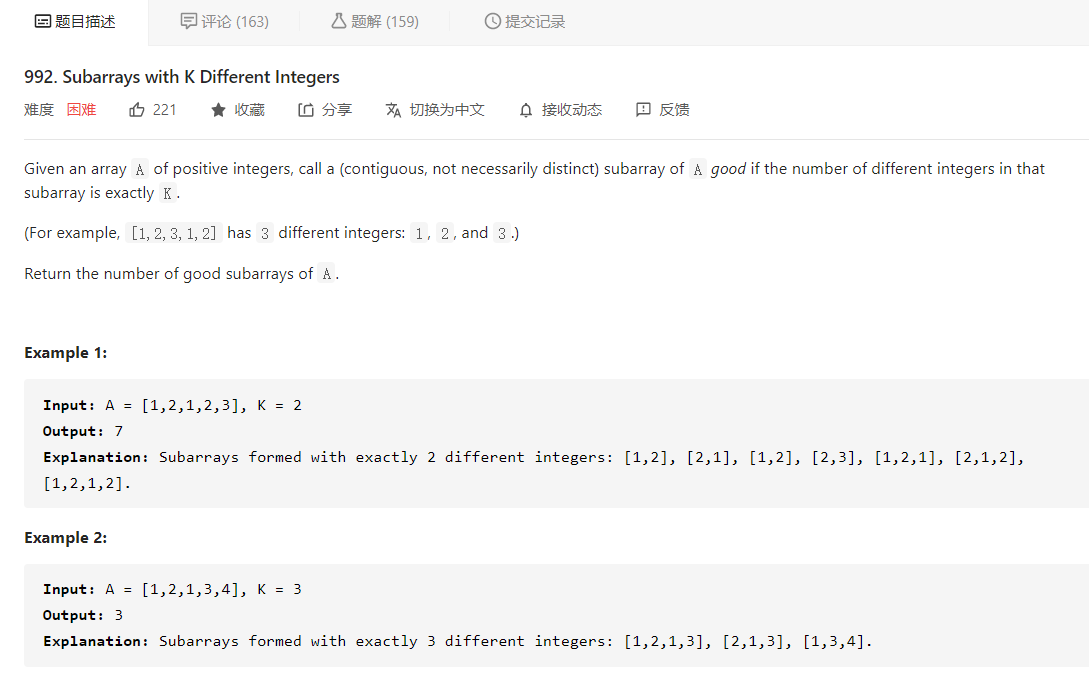
LeetCode每日一题，992. Subarrays With K Different Integers

先看题目描述

yav2gs.png

大意就是给定一个数组 A 和整数 K，让我们计算 A 的包含的不同的数字个数恰好是 K 的子数组的个数

算法和思路

这题一开始用暴力法做的，结果在一个用例那里跑超时了，于是去看题解，才明白要对题目进行转化，就可以使用滑动窗口来解题了

滑动窗口

对比以前我们做过的，使用双指针解决的问题的问法基本都会出现「最小」、「最大」这样的字眼。把「恰好」改成「最多」就可以使用双指针一前一后交替向右的方法完成，这是因为 对于每一个确定的右边界，最多包含 K 种不同整数的左边界是唯一确定的，并且在右边界向右移动的过程中，左边界或者在原来的地方，或者在原来地方的右边

而「最多存在 K 个不同整数的子区间的个数」与「恰好存在 K 个不同整数的子区间的个数」的差恰好等于「最多存在 K − 1 个不同整数的子区间的个数」

因此原问题就转换成为求解「最多存在 K 个不同整数的子区间的个数」与 「最多存在 K − 1 个不同整数的子区间的个数」，它们其实是一个问题

实现一个方法 subarraysWithAtMostKDistinct(A, K)，可以返回数组 A 中至多有 K 个不同数字的子数组的个数，于是 subarraysWithAtMostKDistinct(A, K) - subarraysWithAtMostKDistinct(A, K - 1) 即为所求

算法源码

滑动窗口

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int subarraysWithKDistinct(int[] A, int K) {
        return subarraysWithAtMostKDistinct(A, K) - subarraysWithAtMostKDistinct(A, K - 1);
    }

    private int subarraysWithAtMostKDistinct(int[] A, int K) {
        int len = A.length;
        int count = 0;
        int ans = 0;
        int left = 0;
        int right = 0;
        int[] cnt = new int[len + 1];
        while (right < len) {
            int num = A[right];
            if (cnt[num] == 0) {
                count++;
            }
            cnt[num]++;
            right++;
            while (count > K) {
                cnt[A[left]]--;
                if (cnt[A[left]] == 0) {
                    count--;
                }
                left++;
            }
            ans += right - left;
        }
        return ans;
    }
}

对于 ans += right - left 的理解：以数组 A = [1, 2, 1, 2, 3]，K = 2 为例，初始时 left = 0, right = 0，第一次迭代后 left = 0, right = 1，此时 A[0: 1) 内的不同数字个数是小于等于 K 的，以 A[0] = 1 为右边界的符合要求的子数组只有 right - left = 1 个，是 [1]，于是 ans 加 1；right 接着右移到 left = 0，right = 2， 此时 A[0: 2) 内的不同数字个数是小于等于 K 的，以 A[1] = 2 为右边界的符合要求的子数组有 right - left = 2 个，是 [2]，[1, 2]，于是 ans 再加 2 等于 3；right 再右移到 left = 0，right = 3， 此时 A[0: 3) 内的不同数字个数是小于等于 K 的，以 A[2] = 1 为右边界的符合要求的子数组有 right - left = 3 个，是 [1]，[2, 1]，[1, 2, 1]，于是 ans 再加 3 等于 6；right 就这样右移直至 left = 0，right = 5，此时 A[0: 5) 内的不同数字个数大于 K，将 left 右移到 left = 3，right = 5，这时 A[3: 5) 内的不同数字个数小于等于 K，以 A[4] 为右边界的符合要求的子数组有 right - left = 2 个，于是 ans 再加 2 等于 12。就求出了 A 的最多存在 K 个不同整数的子区间的个数

注意：这题的关键点有两个，第一个是将原问题转换成为求解「最多存在 K 个不同整数的子区间的个数」与 「最多存在 K − 1 个不同整数的子区间的个数」，从而使用滑动窗口来对问题求解；第二个就是对求解「最多存在 K 个不同整数的子区间的个数」中 ans += right - left 的理解