最长湍流子数组

发表于
本文字数： 2k 阅读时长 ≈ 2 分钟

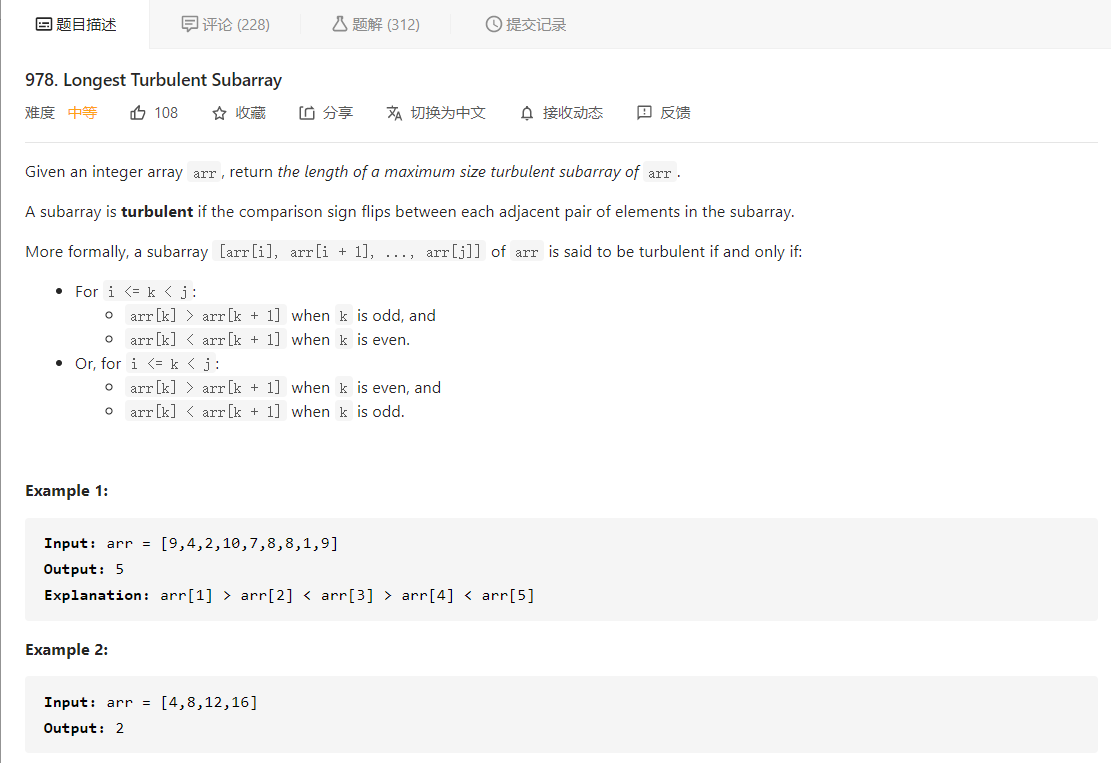
LeetCode每日一题，978.Longest Turbulent Subarray

先看题目描述

yUmzSx.png

大意就是给定一个数组 arr，让我们求出 arr 的最长湍流子数组的长度，湍流子数组的定义是其中的元素呈现一高一低的趋势

算法和思路

双指针

定义两个指针 left 和 right，left 初始化为 0，right 初始化为 1，以 left 为左边界，移动 right 指针来寻找以 left 为左边界的最长湍流子数组，那么 right 停止移动时 arr[left:right) 就是以 left 为左边界的最长湍流子数组(right 为开区间)，此时移动 left 指针来选定进行判断的下一个湍流子数组的左边界，若 arr[right] 与 arr[right - 1] 相等，则移动 left 到 right，否则移动 left 到 right - 1，然后再进行以此时的 left 为左边界的湍流数组的判断，就这样重复该过程直至不可能出现更长的答案

算法源码

双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Solution {
    public int maxTurbulenceSize(int[] arr) {
        int len = arr.length;
        int left = 0;
        int right = 1;
        int max = 1;
        boolean flag = true;
        while (len - left > max) {
            right = left + 1;
            if (arr[right] > arr[left]) {
                flag = true;
            } else if (arr[right] < arr[left]) {
                flag = false;
            } else {
                left = right;
                continue;
            }
            while (right < len) {
                if (flag) {
                    if (arr[right] > arr[right - 1]) {
                        right++;
                        flag = false;
                    } else {
                        break;
                    }
                } else {
                    if (arr[right] < arr[right - 1]) {
                        right++;
                        flag = true;
                    } else {
                        break;
                    }
                }
            }
            max = Math.max(max, right - left);
            if (right == len) {
                break;
            }
            if ((right - left) == 1) {
                left = right;
            } else {
                if (arr[right] == arr[left]) {
                    left = right;
                } else {
                    left = right - 1;
                }
            }
        }
        return max;
    }
}