保证图可完全遍历

发表于
本文字数： 2.9k 阅读时长 ≈ 3 分钟

LeetCode每日一题，1579. Remove Max Number of Edges to Keep Graph Fully Traversable

先看题目描述

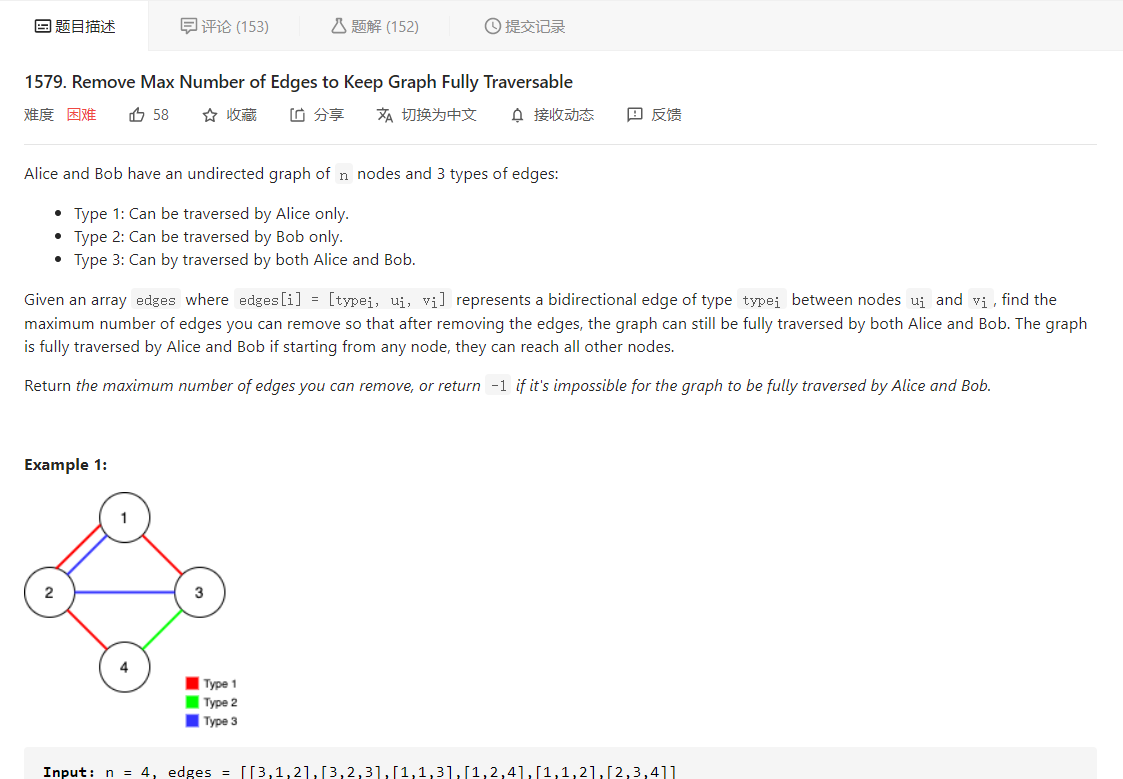
sx8hNQ.png

大意就是有三种类型的边，类型 1 的边是只有 Alice 可访问，类型 2 的边是只有 Bob 可访问，类型 3 的边是两人均可访问，现在给定一个图，问我们最多可以删除多少条边，使 Alice 和 Bob 均可以遍历整张图

算法和思路

并查集

首先要理解题目的意思，题目的意思是当图中只有 Alice 独占边和公共边时，整个图是连通的，同样对于 Bob，当图中只有 Bob 独占边和公共边时，整个图是连通的

看到与连通分量相关的题，就想到可以用并查集，并查集支持合并和查找根节点的操作，可以用于将两个连通分量合并，于是想到可以进行逆向操作，从一个仅包含 n 个节点(不含边)的图开始，逐步添加边，使得满足上述要求

算法流程如下：

  • 遵从优先添加公共边的策略，遍历所有公共边，对于其连接的两个子节点：
    • 若这两个节点在一个连通分量中，则代表该边可以删除
    • 若这两个节点不在一个连通分量中，则保留该边，并将这两个节点所属的连通分量合并
  • 之后分别为 Bob 独占边和 Alice 独占边复制两个当前并查集 unionFind1 和 unionFind2
  • 遍历所有边：
    • 若该边是 Bob 独占边，对于其连接的两个子节点：
      • 若这两个边在一个连通分量中，则代表该边可以删除
      • 若这两个节点不在一个连通分量中，则保留该边，并用 unionFind1 将这两个节点所属的连通分量合并
    • 若该边是 Alice 独占边，对于其连接的两个子节点：
      • 若这两个边在一个连通分量中，则代表该边可以删除
      • 若这两个节点不在一个连通分量中，则保留该边，并用 unionFind2 将这两个节点所属的连通分量合并
  • 最后判断 unionFind1 和 unionFind2 是否均只有一个连通分量，若都只有一个连通分量，则代表 Alice 和 Bob 都可以遍历整个图，返回删除边的数量；否则说明其中有人不能遍历整个图，返回 -1

算法源码

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution {
    public int maxNumEdgesToRemove(int n, int[][] edges) {
        int ans = 0;
        UnionFind unionFind = new UnionFind(n);
        for (int[] edge : edges) {
            if (edge[0] != 3) {
                continue;
            }
            if (!unionFind.union(edge[1], edge[2])) {
                ans++;
            }
        }
        UnionFind unionFind1 = new UnionFind(unionFind);
        UnionFind unionFind2 = new UnionFind(unionFind);
        for (int[] edge : edges) {
            if (edge[0] == 1) {
                if (!unionFind1.union(edge[1], edge[2])) {
                    ans++;
                }
            } else if (edge[0] == 2) {
                if (!unionFind2.union(edge[1], edge[2])) {
                    ans++;
                }
            }
        }
        if (unionFind1.getCount() != 1 || unionFind2.getCount() != 1) {
            return -1;
        }
        return ans;
    }

    private class UnionFind {
        int count;
        int[] parent;

        UnionFind(int n) {
            this.count = n;
            this.parent = new int[n + 1];
            for (int i = 0; i <= n; i++) {
                this.parent[i] = i;
            }
        }

        UnionFind(UnionFind unionFind) {
            this.count = unionFind.getCount();
            this.parent = Arrays.copyOfRange(unionFind.parent, 0, unionFind.parent.length);
        }

        int find(int x) {
            if (x != this.parent[x]) {
                this.parent[x] = find(this.parent[x]);
            }
            return this.parent[x];
        }

        boolean union(int a, int b) {
            int x = find(a);
            int y = find(b);
            if (x == y) {
                return false;
            }
            this.parent[y] = x;
            this.count--;
            return true;
        }

        int getCount() {
            return this.count;
        }
    }
}