等价多米诺骨牌对的数量

发表于
本文字数： 1.8k 阅读时长 ≈ 2 分钟

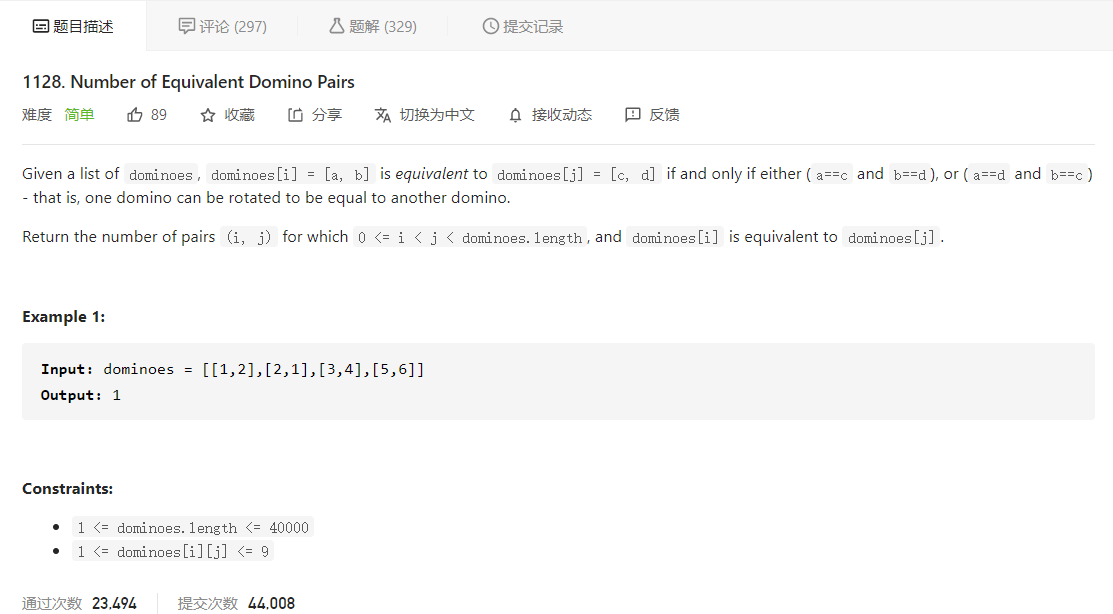
LeetCode每日一题，1128. Number of Equivalent Domino Pairs

先看题目描述

sjZk0x.png

题目大意是给定很多张多米诺骨牌，这些牌用二元组的形式表示，让我们返回等价的多米诺骨牌对的数量，等价的定义是：在允许翻转二元组的情况下，它们的元素一一对应相等

算法和思路

排序

我们先将二元对变为指定的格式，即第一维不大于第二维，于是二元组等价当且仅当二元组完全相等

然后对这些二元组排序，因为完全相同的二元组一定会在相邻位置，于是只需遍历排序后的二元组，每次将当前遍历的二元组与前一个二元组比较即可

计数

同样先将二元对变为指定的格式，即第一维不大于第二维，于是二元组等价当且仅当二元组完全相等

注意到二元组中的元素均不大于 9，于是我们可以将二元组拼接为二位的正整数，即 (x，y) -> 10x + y，这样就不需要用哈希表统计数量，用长度为 100 的整型数组即可

算法源码

排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int numEquivDominoPairs(int[][] dominoes) {
        int len = dominoes.length;
        if (len <= 1) {
            return 0;
        }
        for (int[] domino : dominoes) {
            if (domino[0] > domino[1]) {
                int temp = domino[1];
                domino[1] = domino[0];
                domino[0] = temp;
            }
        }
        Arrays.sort(dominoes, (a, b) -> a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);
        int ans = 0;
        int cur = 1;
        int preX = dominoes[0][0];
        int preY = dominoes[0][1];
        for (int i = 1; i < len; i++) {
            int x = dominoes[i][0];
            int y = dominoes[i][1];
            if (x == preX && y == preY) {
                ans += cur;
                cur++;
            } else {
                cur = 1;
                preX = x;
                preY = y;
            }
        }
        return ans;
    }
}

计数

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int numEquivDominoPairs(int[][] dominoes) {
        int ans = 0;
        int[] count = new int[100];
        for (int[] domino : dominoes) {
            int val = domino[0] < domino[1] ? 10 * domino[0] + domino[1] : 10 * domino[1] + domino[0];
            ans += count[val];
            count[val]++;
        }
        return ans;
    }
}