由斜杠划分区域

发表于
本文字数： 2.7k 阅读时长 ≈ 2 分钟

LeetCode每日一题，959. Regions Cut By Slashes

先看题目描述

sX835R.png

大意就是给定一个 N * N 的网格，网格会被斜杠或反斜杠给划分成不同的区域，让我们返回区域的个数

算法和思路

并查集

看到这题，我们很容易就想到可以使用并查集来求连通分量的个数

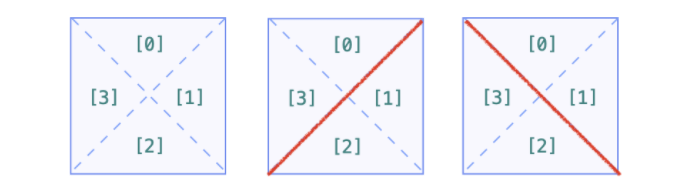
斜杠、反斜杠把单元格拆分成两个三角形的形态，在做合并的时候需要分类讨论。根据斜杠与反斜杠分割的特点，我们把一个单元格分成逻辑上的四部分，如下所示：

sXGly8.png

我们需要遍历一次输入的二维网格 grid，在单元格内和单元格间进行合并

接下来我们考虑在单元格内和单元格间合并的情况

单元格内合并：

  • 若此时该单元格内是 “/“，则将 0、3 合并，1、2 合并
  • 若此时单元格内是 “\\“，则将 0、1 合并，2、3 合并
  • 若单元格内为空，则直接 0、1、2、3 一起合并

单元格间合并：

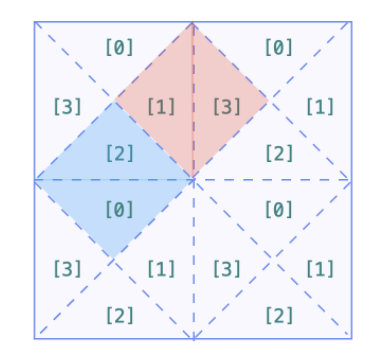
单元格间的合并就考虑将每个单元格向右和向下合并，即将当前单元格的 1 和右边单元格的 3 合并，当前单元格的 2 和下方单元格的 0 合并，如下图所示

sXJ7uT.png

合并完成以后，返回连通分量的个数即可，连通分量的个数就是划分区域的个数

算法源码

并查集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
class Solution {
    public int regionsBySlashes(String[] grid) {
        final int N = grid.length;
        int size = 4 * N * N;
        
        UnionFind unionFind = new UnionFind(size);
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < N; j++) {
                // 二维表格转化为一维表格
                int index = 4 * (i * N + j);
                char c = grid[i].charAt(j);
                // 单元格内合并
                if (c == '/') {
                    unionFind.union(index, index + 3);
                    unionFind.union(index + 1, index + 2);
                } else if (c == '\\') {
                    unionFind.union(index, index + 1);
                    unionFind.union(index + 2, index + 3);
                } else {
                    unionFind.union(index, index + 1);
                    unionFind.union(index + 1, index + 2);
                    unionFind.union(index + 2, index + 3);
                }

                // 单元格间合并
                // 向右合并：1（当前）、3（右一列）
                if (j < N - 1) {
                    unionFind.union(index + 1, index + 7);
                }
                // 向下合并：2（当前）、0（下一行）
                if (i < N - 1) {
                    unionFind.union(index + 2, index + 4 * N);
                }
            }
        }
        return unionFind.getCount();
    }

    private class UnionFind {
        int count;
        int[] parent;

        UnionFind(int count) {
            this.count = count;
            this.parent = new int[count];
            for (int i = 0; i < count; i++) {
                this.parent[i] = i;
            }
        }

        int find(int x) {
            if (x != this.parent[x]) {
                this.parent[x] = find(this.parent[x]);
            }
            return this.parent[x];
        }

        void union(int a, int b) {
            int x = find(a);
            int y = find(b);
            if (x == y) {
                return;
            }
            this.parent[y] = x;
            this.count--;
        }

        int getCount() {
            return this.count;
        }
    }
}