找到最小生成树的关键边和伪关键边

发表于
本文字数： 3.9k 阅读时长 ≈ 4 分钟

LeetCode每日一题，1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree

先看题目描述

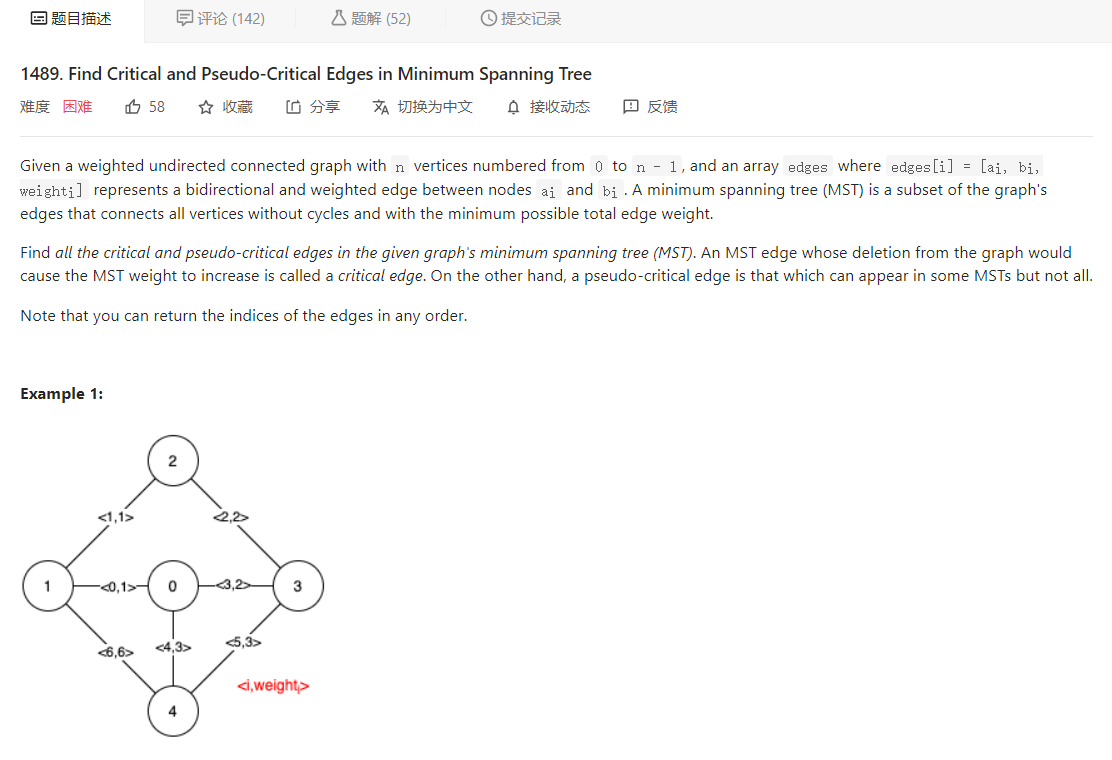
sh6pRK.png

大意就是给定一个数字 n 代表共有 n 个节点，一个二维数组 edges 代表边集，edges 中的某个元素 [i，j，len] 代表 节点 i 和节点 j 之间有个长度为 len 的边，让我们找出图中最小生成树的所有关键边和伪关键边

算法和思路

枚举 + 最小生成树判定

我们首先需要关键边和伪关键边的定义

  • 关键边：如果最小生成树中删去某条边，会导致最小生成树的权值和增加，那么我们就说它是一条关键边。也就是说，如果设原图最小生成树的权值为 value，那么去掉这条边后：
    • 要么整个图不连通，不存在最小生成树；
    • 要么整个图联通，对应的最小生成树的权值为 v，其值严格大于 value
  • 伪关键边：可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。也就是说，我们可以在计算最小生成树的过程中，最先考虑这条边，即最先将这条边的两个端点在并查集中合并。设最终得到的最小生成树权值为 v，如果 v = value，那么这条边就是伪关键边

需要注意的是，关键边也满足伪关键边对应的性质。因此，我们首先对原图执行 Kruskal 算法，得到最小生成树的权值 value，随后我们枚举每一条边，首先根据上面的方法判断其是否是关键边，如果不是关键边，再判断其是否是伪关键边

算法源码

枚举 + 最小生成树判定

这实际上就是暴力法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
class Solution {
    private int[] parent;

    public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
        int len = edges.length;
        List<List<Integer>> res = new ArrayList<>();
        res.add(new ArrayList<>());
        res.add(new ArrayList<>());
        List<Edge> edgeList = new ArrayList<>();
        this.parent = new int[n];
        for (int i = 0; i < n; i++) {
            this.parent[i] = i;
        }
        for (int i = 0; i < len; i++) {
            Edge edge = new Edge(i, edges[i][0], edges[i][1], edges[i][2]);
            edgeList.add(edge);
        }
        Collections.sort(edgeList, (a, b) -> a.len - b.len);
        int value = 0;
        int count = 1;
        for (int i = 0; i < len; i++) {
            if (union(edgeList.get(i).x, edgeList.get(i).y)) {
                value += edgeList.get(i).len;
                count++;
            }
            if (count == n) {
                break;
            }
        }
        for (int i = 0; i < len; i++) {
            for (int j = 0; j < n; j++) {
                this.parent[j] = j;
            }
            Edge edge1 = edgeList.get(i);
            int v = 0;
            int num = 1;
            for (int j = 0; j < len; j++) {
                if (j == i) {
                    continue;
                }
                Edge edge2 = edgeList.get(j);
                if (union(edge2.x, edge2.y)) {
                    v += edge2.len;
                    num++;
                }
                if (num == n) {
                    break;
                }
            }
            if (num < n || v > value) {
                res.get(0).add(edge1.index);
                continue;
            }
            for (int j = 0; j < n; j++) {
                this.parent[j] = j;
            }
            num = 2;
            union(edge1.x, edge1.y);
            v = edge1.len;
            for (int j = 0; j < len; j++) {
                Edge edge3 = edgeList.get(j);
                if (num == n) {
                    break;
                }
                if (j == i) {
                    continue;
                }
                if (union(edge3.x, edge3.y)) {
                    v += edge3.len;
                    num++;
                }
            }
            if (v == value) {
                res.get(1).add(edge1.index);
            }
        }
        return res;
    }

    private int find(int x) {
        if (x != this.parent[x]) {
            this.parent[x] = find(this.parent[x]);
        }
        return this.parent[x];
    }

    private boolean union(int a, int b) {
        int x = find(a);
        int y = find(b);
        if (x == y) {
            return false;
        }
        this.parent[y] = x;
        return true;
    }

    private class Edge {
        int index;
        int x;
        int y;
        int len;

        Edge(int index, int x, int y, int len) {
            this.index = index;
            this.x = x;
            this.y = y;
            this.len = len;
        }
    }
}