连接所有点的最小费用(求最小生成树的权值)

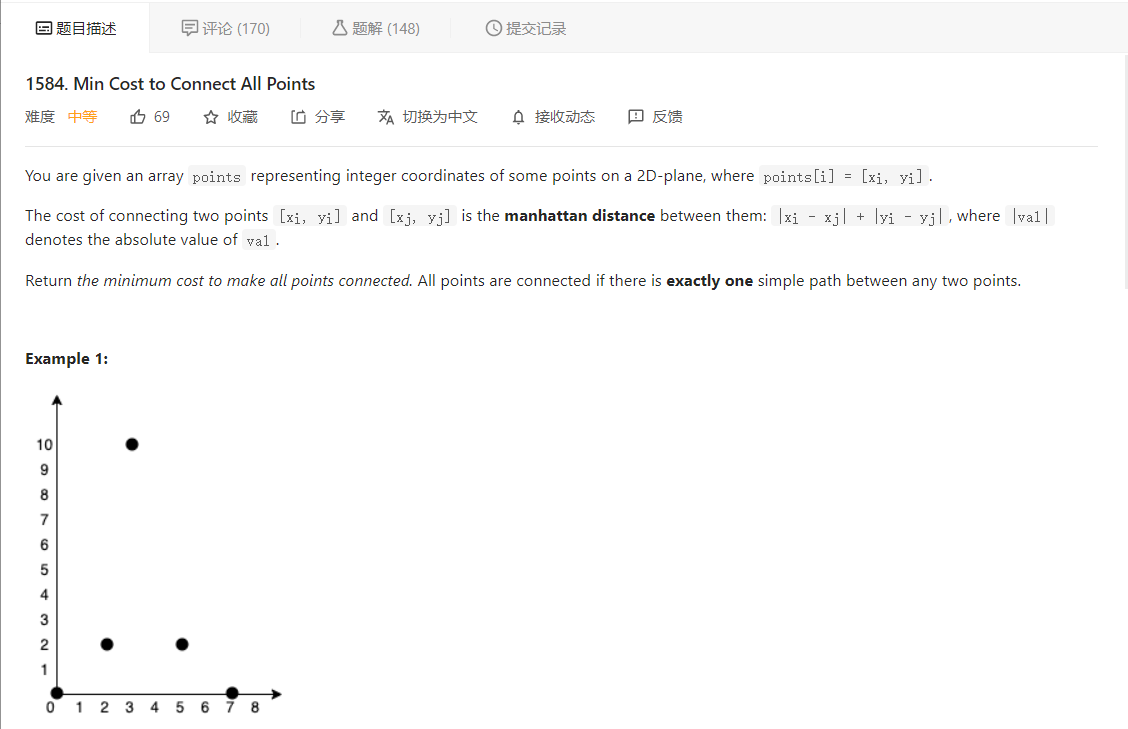
LeetCode题目，1584. Min Cost to Connect All Points

先看题目描述

大意就是给定很多个二维点的坐标，连接点的费用是这两个点之间的曼哈顿距离，问将所有点连通的最小花费是多少

算法和思路

这题本质上就是给定一个图，让我们求出这个图的最小生成树，并将最小生成树的权值返回，求最小生成树有两个很经典的算法，Kruskal 算法 和 Prim 算法

Kruskal 算法的基本思路是从小到大加入边，直至得到最小生成树，本质是一个贪心算法

Prim 算法的基本思路是将点分为两类，A 类是已经在树中的点，其他的点是 B 类，初始时 A 类中只有第一个点，每次都从 B 类中选出若要加入 A 类花费的代价最小的点加入 A 类，直至 B 类点为空，得到最小生成树，这也是一个贪心算法

算法源码

这两个算法中都使用了并查集，用于判断边的两顶点是否在一个连通分量中

Kruskal 算法

class Solution {
    public int minCostConnectPoints(int[][] points) {
        int n = points.length;
        int[] parent = new int[n];
        List<Edge> edges = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                edges.add(new Edge(i, j, getManhattan(points[i], points[j])));
            }
        }
        Collections.sort(edges, (a, b) -> a.len - b.len);
        int res = 0;
        int num = 1;
        for (Edge edge : edges) {
            if (find(edge.x, parent) == find(edge.y, parent)) {
                continue;
            }
            union(edge.x, edge.y, parent);
            res += edge.len;
            num++;
            if (num == n) {
                break;
            }
        }
        return res;
    }

    private int getManhattan(int[] point1, int[] point2) {
        return Math.abs(point1[0] - point2[0]) + Math.abs(point1[1] - point2[1]);
    }

    private int find(int x, int[] parent) {
        if (x != parent[x]) {
            parent[x] = find(parent[x], parent);
        }
        return parent[x];
    }

    private void union(int a, int b, int[] parent) {
        int x = find(a, parent);
        int y = find(b, parent);
        parent[y] = x;
    }

    private class Edge {
        int x;
        int y;
        int len;

        Edge(int x, int y, int len) {
            this.x = x;
            this.y = y;
            this.len = len;
        }
    }
}

Prim 算法

class Solution {
    public int minCostConnectPoints(int[][] points) {
        int res = 0;
        int n = points.length;
        int[] parent = new int[n];
        PriorityQueue<Edge> prior = new PriorityQueue<Edge>(new Comparator<Edge>() {
            @Override
            public int compare(Edge o1, Edge o2) {
                return o1.len - o2.len;
            }
        });
        Map<Integer, List<Edge>> map = new HashMap<>();
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            map.put(i, new ArrayList<>());
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                Edge edge = new Edge(i, j, getManhattan(points[i], points[j]));
                map.get(i).add(edge);
                map.get(j).add(edge);
            }
        }
        for (Edge edge : map.get(0)) {
            prior.offer(edge);
        }
        for (int i = 1; i < n; i++) {
            Edge edge = prior.poll();
            while (find(edge.x, parent) == find(edge.y, parent)) {
                edge = prior.poll();
            }
            res += edge.len;
            int index = find(edge.x, parent) == 0 ? edge.y : edge.x;
            union(0, index, parent);
            for (Edge e : map.get(index)) {
                if (find(e.x, parent) == find(e.y, parent)) {
                    continue;
                }
                prior.add(e);
            }
        }
        return res;
    }

    private int getManhattan(int[] point1, int[] point2) {
        return Math.abs(point1[0] - point2[0]) + Math.abs(point1[1] - point2[1]);
    }

    private int find(int x, int[] parent) {
        if (x != parent[x]) {
            parent[x] = find(parent[x], parent);
        }
        return parent[x];
    }

    private void union(int a, int b, int[] parent) {
        int x = find(a, parent);
        int y = find(b, parent);
        parent[y] = x;
    }

    private class Edge {
        int x;
        int y;
        int len;

        Edge(int x, int y, int len) {
            this.x = x;
            this.y = y;
            this.len = len;
        }
    }
}