打砖块

发表于 更新于
本文字数： 7.8k 阅读时长 ≈ 7 分钟

LeetCode每日一题，803. Bricks Falling When Hit

先看题目描述

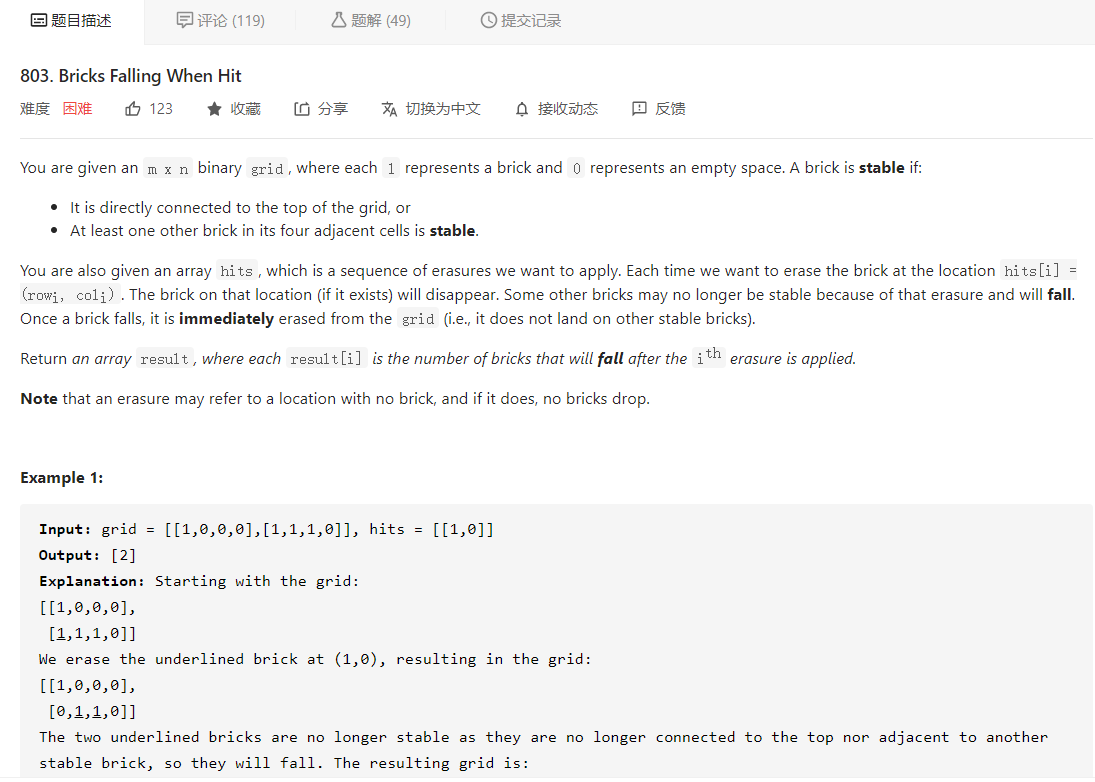
sDUGKs.png

大意就是给定一个只包含 1 和 0 的二维矩阵，其中 1 代表 砖块，0 代表空地，一个砖块是稳定的得满足下面两个条件之一：

  • 该砖块直接与二维矩阵顶部相连
  • 该砖块相邻的砖块中至少有一个是稳定的

给定 hits 数组代表要敲除的砖块的位置，一个砖块敲除后，可能有一些其他砖块变得不稳定而掉落，让我们返回数组 result，result[i] 代表第 i 个砖块被敲除后，掉落的其他砖块数量

算法和思路

并查集

这题不会，看题解才会的

如何想到并查集

  • 当前问题是一个图的连通性问题，砖块和砖块如果在 4 个方向上相邻，表示这两个砖块上有一条边。砖块的相邻关系而产生的连接关系具有传递性；
  • 第 0 行的砖块连接着「屋顶」；
  • 击碎了一个砖块以后，可能会使得其它与「被击碎砖块」 连接 的砖块不再与顶部相连，然后它们消失；
    题目只问结果，没有问具体连接的情况；
  • 连通的砖块个数是我们所关心的，「并查集」内部可以维护「以当前结点为根结点的子树的结点总数」

如何使用并查集

  • 消除一个砖块的效果是：一个连通分量被分成了两个连通分量；
  • 并查集的作用是：把两个连通分量合并成一个连通分量

提示我们这个问题需要 反向 思考。即考虑：补上被击碎的砖块以后，有多少个砖块因为这个补上的这个砖块而与屋顶的砖块相连。每一次击碎一个砖块，因击碎砖块而消失的砖块只会越来越少。因此可以按照数组 hits 的顺序 逆序地 把这些砖块依次补上

步骤

  • 根据数组 hits，将输入的表格 grid 里的对应位置全部设置为 0 ，这是因为我们要逆序补全出整个初始化的时候二维表格的砖块；
  • 从最后一个击碎的砖块开始，计算补上这个被击碎的砖块的时候，有多少个砖块因为这个补上的砖块而与屋顶相连，这个数目就是按照题目中的描述，击碎砖块以后掉落的砖块的数量

实现细节

  • 在并查集中设置一个特殊的结点，表示「屋顶」；
  • 逆序补回的时候，由于补回，增加的连接到「屋顶」的砖块数应该这样算：res[i] = Math.max(0, current - origin - 1); 因为有可能补回一个砖块前后，连接到「屋顶」的砖块总数没有变化

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
class Solution {
    public int[] hitBricks(int[][] grid, int[][] hits) {
        final int[][] Directions = {{-1, 0}, {0, 1}, {1, 0}, {0, - 1}};
        int len = hits.length;
        int[] res= new int[len];
        int m = grid.length;
        int n = grid[0].length;
        int size = m * n;
        int[] parent = new int[size + 1];
        int[] count = new int[size + 1];
        for (int i= 0; i <= size; i++) {
            parent[i] = i;
            count[i] = 1;
        }
        count[size] = 0;
        int[][] copy = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                copy[i][j] = grid[i][j];
            }
        }
        for (int[] hit : hits) {
            copy[hit[0]][hit[1]] = 0;
        }
        for (int i = 0; i < n; i++) {
            if (copy[0][i] == 1) {
                union(size, i, parent, count);
            }
        }
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (copy[i][j] == 0) {
                    continue;
                }
                if (copy[i - 1][j] == 1) {
                    union(getIndex(i - 1, j, n), getIndex(i, j, n), parent, count);
                }
                if (isInArea(i, j - 1, m, n) && copy[i][j - 1] == 1) {
                    union(getIndex(i, j - 1, n), getIndex(i, j, n), parent, count);
                }
            }
        }
        for (int i = len - 1; i >= 0; i--) {
            int x = hits[i][0];
            int y = hits[i][1];
            if (grid[x][y] == 0) {
                continue;
            }
            int origin = getCount(size, parent, count);
            copy[x][y] = 1;
            if (x == 0) {
                union(size, getIndex(x, y, n), parent, count);
            }
            for (int j = 0; j < 4; j++) {
                int nx = x + Directions[j][0];
                int ny = y + Directions[j][1];
                if (isInArea(nx, ny, m, n) && copy[nx][ny] == 1) {
                    union(getIndex(nx, ny, n), getIndex(x, y, n), parent, count);
                }
            }
            int current = getCount(size, parent, count);
            res[i] = Math.max(0, current - origin - 1);
        }
        return res;
    }

    private boolean isInArea(int x, int y, int m, int n) {
        return x >= 0 && x < m && y >= 0 && y < n;
    }

    private int getIndex(int x, int y, int n) {
        return x * n + y;
    }

    private int find(int x, int[] parent) {
        if (x != parent[x]){
            parent[x] = find(parent[x], parent);
        }
        return parent[x];
    }

    private void union(int a, int b, int[] parent, int[] count) {
        int x = find(a, parent);
        int y = find(b, parent);
        if (x == y) {
            return;
        }
        parent[y] = x;
        count[x] += count[y];
    }
    
    private int getCount(int x, int[] parent, int[] count) {
        int root = find(x, parent);
        return count[root];
    }
}

下面是将并查集作为内部类的写法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
class Solution {
    final int[][] DIRECTIONS = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
    private int m;
    private int n;

    public int[] hitBricks(int[][] grid, int[][] hits) {
        this.m = grid.length;
        this.n = grid[0].length;
        int size = this.m * this.n;
        int len = hits.length;
        int[] res = new int[len];
        int[][] copy = new int[this.m][this.n];
        UnionFind unionFind = new UnionFind(size + 1);
        for (int i = 0; i < this.m; i++) {
            for (int j = 0; j < this.n; j++) {
                copy[i][j] = grid[i][j];
            }
        }
        for (int[] hit : hits) {
            copy[hit[0]][hit[1]] = 0;
        }
        for (int i = 0; i < this.n; i++) {
            if (copy[0][i] == 0) {
                continue;
            }
            unionFind.union(size, i);
        }
        for (int i = 1; i < this.m; i++) {
            for (int j = 0; j < this.n; j++) {
                if (copy[i][j] == 0) {
                    continue;
                }
                if (copy[i - 1][j] == 1) {
                    unionFind.union(getIndex(i - 1, j), getIndex(i, j));
                }
                if (isInArea(i, j - 1) && copy[i][j - 1] == 1) {
                    unionFind.union(getIndex(i, j - 1), getIndex(i, j));
                }
            }
        }
        for (int i = len - 1; i >= 0; i--) {
            int x = hits[i][0];
            int y = hits[i][1];
            if (grid[x][y] == 0) {
                continue;
            }
            copy[x][y] = 1;
            int origin = unionFind.getCount(size);
            if (x == 0) {
                unionFind.union(size, y);
            }
            for (int j = 0; j < 4; j++) {
                int nx = x + this.DIRECTIONS[j][0];
                int ny = y + this.DIRECTIONS[j][1];
                if (isInArea(nx, ny) && copy[nx][ny] == 1) {
                    unionFind.union(getIndex(nx, ny), getIndex(x, y));
                }
            }
            int current = unionFind.getCount(size);
            res[i] = Math.max(0, current - origin - 1);
        }
        return res;
    }

    private boolean isInArea(int x, int y) {
        return x >= 0 && x < this.m && y >= 0 && y < this.n;
    }

    private int getIndex(int x, int y) {
        return x * this.n + y;
    }

    private class UnionFind {
        int[] parent;
        int[] count;

        UnionFind(int size) {
            this.parent = new int[size];
            this.count = new int[size];
            for (int i= 0; i < size; i++) {
                this.parent[i] = i;
                this.count[i] = 1;
            }
            this.count[size - 1] = 0;
        }

        int find(int x) {
            if (x != this.parent[x]) {
                this.parent[x] = find(this.parent[x]);
            }
            return this.parent[x];
        }

        void union(int a, int b) {
            int x = find(a);
            int y = find(b);
            if (x == y) {
                return;
            }
            this.parent[y] = x;
            this.count[x] += this.count[y];
        }

        int getCount(int x) {
            int root = find(x);
            return this.count[root];
        }
    }
}