冗余连接

发表于
本文字数： 1.5k 阅读时长 ≈ 1 分钟

LeetCode每日一题，684. Redundant Connection

先看题目描述

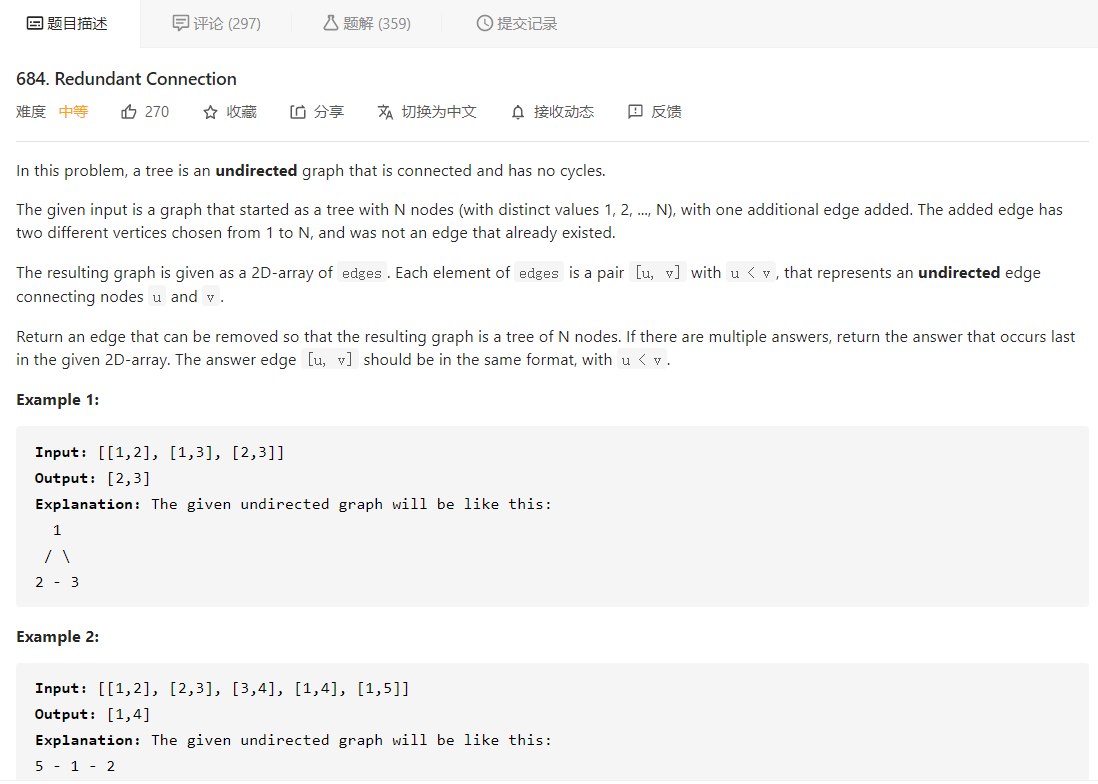
sNL0nx.png

大意就是给定一个无向图，该图由一个有 N 个节点的树和一条附加边构成，附加边的两个顶点在 1 到 N 之间，这条附加的边不属于树中已存在的边。让我们返回一条可以删除的边，使得结果图是一个有 N 个节点的树，若有多条可删除的边，则返回最后出现的边

算法和思路

并查集

在一棵树中，边的数量比节点的数量少 1。如果一棵树有 N 个节点，则该数有 N - 1 条边。该题中的图在树的基础上添加了一条附加边，故共有 N 条边

树是一个连通且无环的无向图，在树中添加一条附加边后便会出现环，因此附加的边即为导致环出现的边

我们可以通过并查集寻找附加的边。初始时，每个节点属于不同的连通分量。遍历每一条边，判断这条边的两个顶点是否属于不同的连通分量：

  • 若两个顶点属于不同的连通分量，则说明在遍历到这条边之前，两个顶点不连通，因此当前的边不会导致环出现，将这两个顶点所属的连通分量合并
  • 若这两个顶点属于相同的连通分量，则说明在遍历到这条边之前，两个顶点已连通，因此当前的边会导致环的出现，直接将这条边返回

算法源码

并查集

并查集部分的代码中使用了路径压缩，未使用按秩合并

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] parent = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for (int[] edge : edges) {
            int root1 = find(edge[0], parent);
            int root2 = find(edge[1], parent);
            if (root1 == root2) {
                return edge;
            } else {
                parent[root2] = root1;
            }
        }
        return new int[]{1, 1};
    }

    private int find(int x, int[] parent) {
        if (x != parent[x]) {
            parent[x] = find(parent[x], parent);
        }
        return parent[x];
    }

    private void union(int a, int b, int[] parent) {
        int x = find(a, parent);
        int y = find(b, parent);
        parent[y] = x;
    }
}