省份数量

发表于
本文字数： 3.5k 阅读时长 ≈ 3 分钟

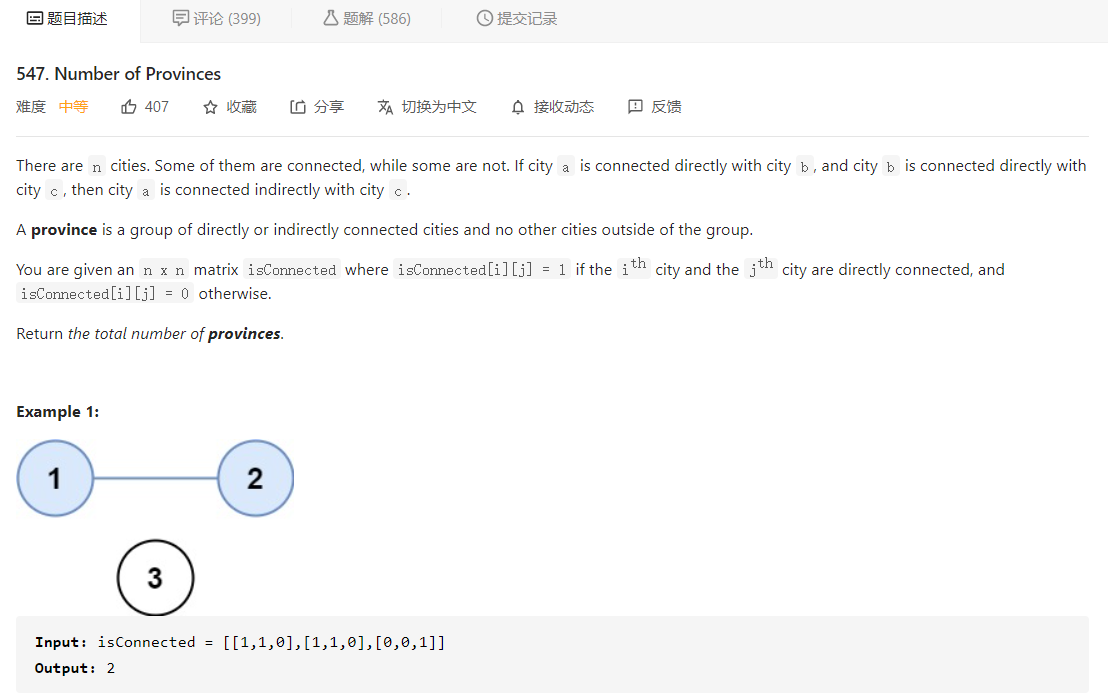
LeetCode每日一题，547. Number of Provinces

先看题目描述

sZqKDU.png

大意就是给定一个图的邻接矩阵，让我们求该图的连通分量的总数

算法和思路

深度优先搜索

遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过邻接矩阵得到该城市的相邻城市，这些城市和该城市属于一个连通分量，然后继续对这些城市继续深度优先搜索，直到一个连通分量内的所有城市均被访问过。遍历完所有城市后，即可得到该图的连通分量的总数

广度优先搜索

这个算法和深度优先搜索的思路差不多，只是搜索方式由深度优先搜索改为了广度优先搜索。遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始广度优先搜索，通过邻接矩阵得到该城市的相邻城市，这些城市和该城市属于一个连通分量，然后继续对这些城市进行广度优先搜索，直到一个连通分量内的所有城市均被访问过。遍历完所有城市后，即可得到该图的连通分量的总数

并查集

这题我们也可以使用并查集，初始时，每个城市属于不同的连通分量，然后我们遍历邻接矩阵，对于每对相邻的城市，我们将其所属的连通分量合并。遍历完邻接矩阵后，我们就可得到该图的连通分量的总数

算法和源码

深度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int res = 0;
        boolean[] visited = new boolean[n];
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                dfs(i, isConnected, visited);
                res++;
            }
        }
        return res;
    }

    private void dfs(int i, int[][] isConnected, boolean[] visited) {
        visited[i] = true;
        for (int j = 0; j < isConnected.length; j++) {
            if (!visited[j] && isConnected[i][j] == 1) {
                dfs(j, isConnected, visited);
            }
        }
    }
}

广度优先搜索

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int res = 0;
        boolean[] visited = new boolean[n];
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < n; i++) {
            if (!visited[i]) {
                queue.offer(i);
                visited[i] = true;
                while (!queue.isEmpty()) {
                    int node = queue.poll();
                    for (int j = 0; j < n; j++) {
                        if (!visited[j] && isConnected[node][j] == 1) {
                            queue.offer(j);
                            visited[j] = true;
                        }
                    }
                }
                res++;
            }
        }
        return res;
    }
}

并查集

实现的并查集算法的代码中使用了路径压缩和按秩合并来优化算法的运行效率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int res = 0;
        int[] parent = new int[n];
        int[] rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            rank[i] = 1;
        }
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                if (isConnected[i][j] == 1) {
                    union(i, j, parent, rank);
                }
            }
        }
        for (int i = 0; i < n; i++) {
            if (parent[i] == i) {
                res++;
            }
        }
        return res;
    }
    
    // 路径压缩，将路径上所有节点的父节点设置为根节点
    private int find(int x, int[] parent) {
        if (x != parent[x]) {
            parent[x] = find(parent[x], parent);
        }
        return parent[x];
    }

    // 按秩合并，将深度小的子树合并到深度更大在子树上，若两子树原深度相同，则将合并后子树的深度加 1
    private void union(int a, int b, int[] parent, int[] rank) {
        int x = find(a, parent);
        int y = find(b, parent);
        if (rank[x] < rank[y]) {
            parent[x] = y;
        } else {
            parent[y] = x;
        }
        if (x != y && rank[x] == rank[y]) {
            rank[x]++;
        }
    }
}