滑动窗口最大值

发表于
本文字数： 1.7k 阅读时长 ≈ 2 分钟

LeetCode每日一题，239. Sliding Window Maximum

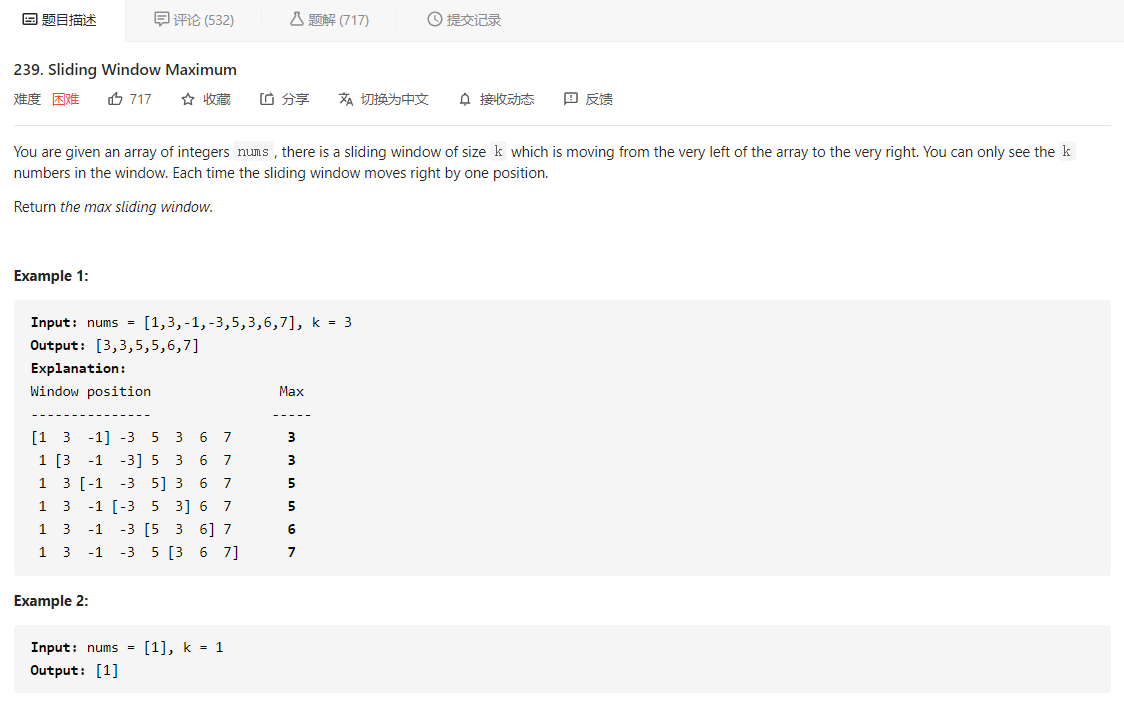
先看题目描述

rzL7PH.png

大意就是给定一个数组 nums，还有一个大小为 k 的窗口从最左侧滑到最右侧，滑动窗口每次只向右移动一位，返回滑动窗口中的最大值

算法和思路

优先队列

看到最大值，很容易就想到用优先队列，可以用优先队列中的大根堆来实时维护一系列元素中的最大值

大致思路就是先将 nums 中的前 k 个元素放入大根堆中，每当我们向右移动滑动窗口时，就把一个新的元素放入大根堆中，此时堆顶元素就是堆中所有元素的最大值，但是堆顶元素不一定在滑动窗口中，若堆顶元素在滑动窗口左边界的左侧，就不在滑动窗口中，此时就不断删除堆顶元素直至堆顶元素在滑动窗口中，然后就找到了此时的滑动窗口中的最大值。每次向右移动滑动窗口时重复此过程即可。为了判断堆顶元素是否在滑动窗口中，我们需要在堆中存储二元组，二元组中放元素的下标和值

算法源码

优先队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int len = nums.length;
        k = Math.min(k, len);
        int[] res = new int[len + 1 - k];
        PriorityQueue<int[]> prior = new PriorityQueue<>((a, b) -> b[0] - a[0]);
        for (int i = 0; i < k; i++) {
            prior.add(new int[]{nums[i], i});
        }
        res[0] = prior.peek()[0];
        for (int i = k; i < len; i++) {
            prior.add(new int[]{nums[i], i});
            while (prior.peek()[1] <= i - k) {
                prior.poll();
            }
            res[i - k + 1] = prior.peek()[0];
        }
        return res;
    }
}

下面是一开始实现的优先队列方法的代码，但是提交的时候跑超时了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int len = nums.length;
        k = Math.min(k, len);
        int[] res = new int[len + 1 - k];
        PriorityQueue<Integer> prior = new PriorityQueue<>((a, b) -> b - a);
        for (int i = 0; i < k - 1; i++) {
            prior.add(nums[i]);
        }
        for (int i = 0; i < len + 1 - k; i++) {
            prior.add(nums[i + k - 1]);
            res[i] = prior.peek();
            prior.remove(nums[i]);
        }
        return res;
    }
}