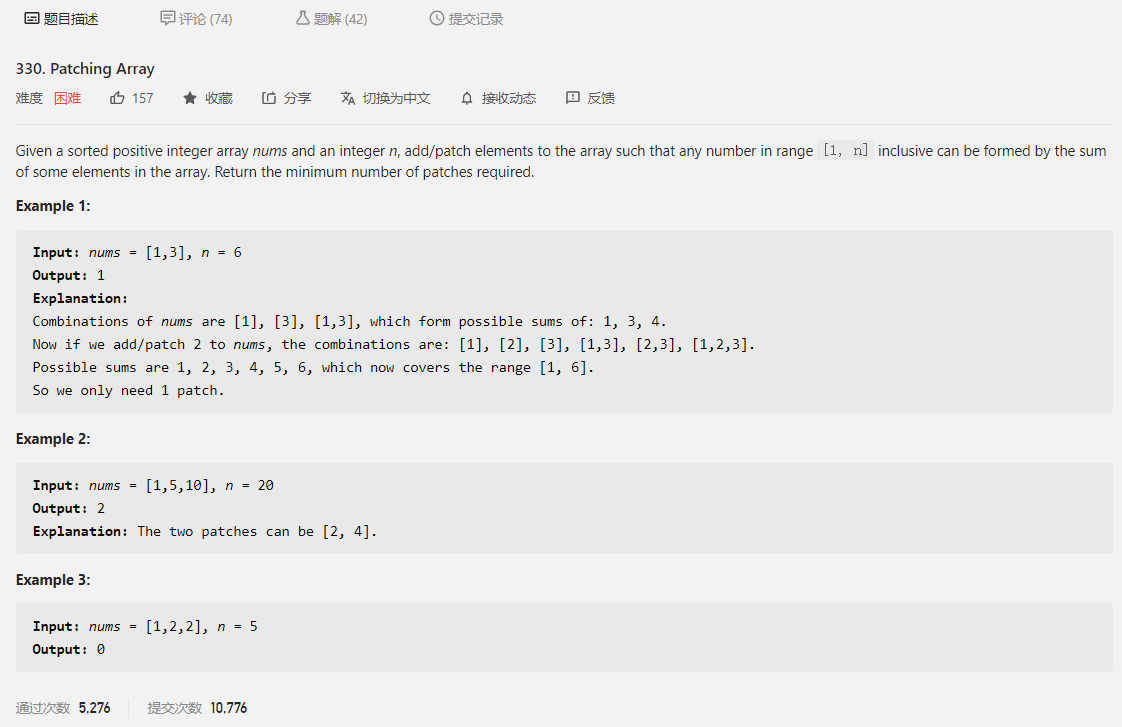
LeetCode每日一题,330. Patching Array
先看题目描述
大意就是给定一个数组 nums 和 一个整数 n,让我们判断若想使 [1,n] 区间内的任何一个数字都可以用 nums 中某几个元素的和来表示,需要在 nums 中添加的元素的最小数量
算法和思路
今天这题又不会,连续两天困难题也太绝望了…今天的题和昨天的题都是看题解才明白的,感觉今天这题主要难在数学部分
贪心算法
对于正整数 x,如果区间 [1,x - 1] 内的所有数字都已经被覆盖,且 x 在数组中,则区间 [1,2x - 1] 内的所有数字也都被覆盖,证明如下:
对于任意 1 <= y < x,y 已经被覆盖,x 在数组中,因此 y + x 也被覆盖,区间 [x + 1,2x - 1] (即区间 [1,x - 1] 内的每个数字加上 x 之后得到的区间) 内的所有数字也被覆盖,由此可得区间 [1,2x + 1] 内的所有数字都被覆盖
假设数字 x 缺失,则至少需要在数组中补充一个小于或等于 x 的数,才能覆盖到 x,否则无法覆盖到 x
如果区间 [1,x−1] 内的所有数字都已经被覆盖,则从贪心的角度考虑,补充 x 之后即可覆盖到 x,且满足补充的数字个数最少。在补充 x之后,区间 [1,2x−1] 内的所有数字都被覆盖,下一个缺失的数字一定不会小于 2x
由此可以提出一个贪心的方案。每次找到未被数组 nums 覆盖的最小的整数 x,在数组中补充 x,然后寻找下一个未被覆盖的最小的整数,重复上述步骤直到区间 [1,n] 中的所有数字都被覆盖
具体实现方面,任何时候都应满足区间 [1,x−1] 内的所有数字都被覆盖。令 x 的初始值为 1,数组下标 index 的初始值为 0,则初始状态下区间 [1,x−1] 为空区间,满足区间内的所有数字都被覆盖。进行如下操作:
- 若 index 在数组 nums 的下标范围内且 nums[index] <= x,则更新 x 为 x + nums[index]
- 被覆盖的区间从 [1,x - 1] 扩展到 [1,x + nums[index] - 1],将 x 的值更新以后,被覆盖的区间为 [1,x - 1]
- 否则,x 没有被覆盖,根据贪心策略,此时需要在数组 nums 中补充 x,并更新 x 为 2x
- 在数组中补充 x 后,被覆盖的区间从 [1,x - 1] 扩展到 [1,2x - 1],将 x 的值更新以后,被覆盖的区间为 [1,x - 1]
- 重复上述操作,直到 x 的值大于 n
算法源码
贪心算法
1 | class Solution { |