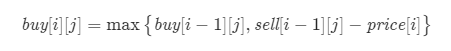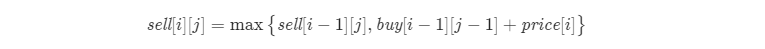LeetCode每日一题,188. Best Time to Buy and Sell Stock IV
先看题目描述
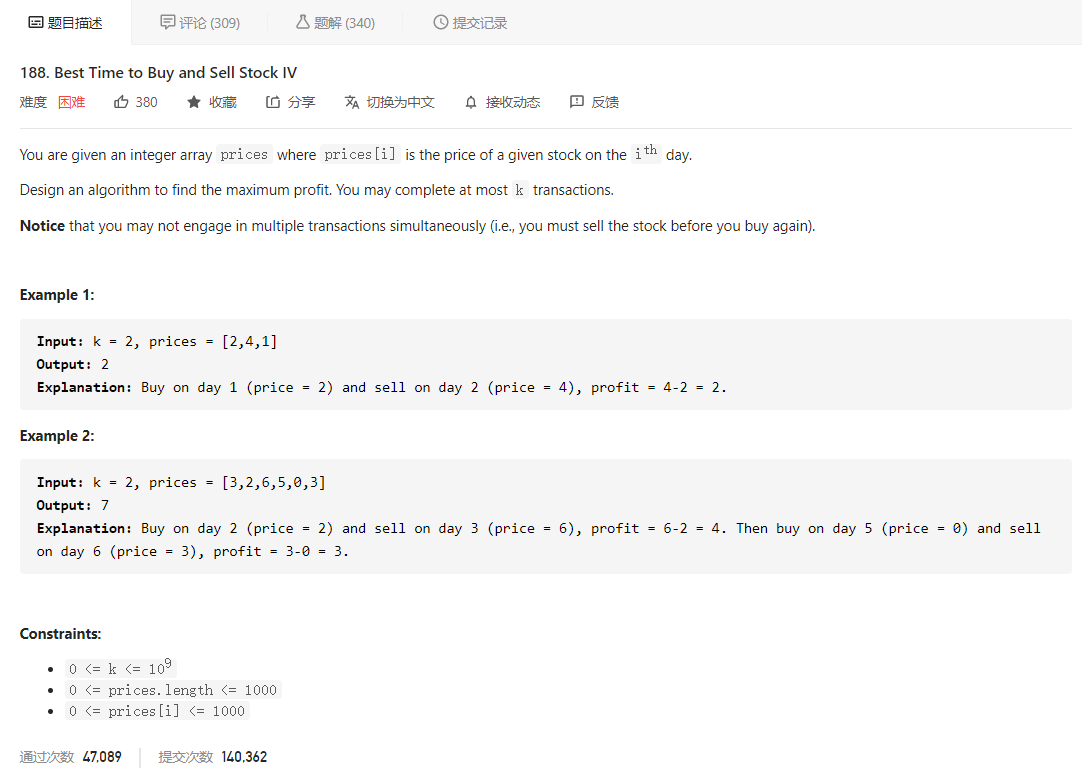
大意就是给定一个数组 prices,代表股票每天的价格,再给定一个整数 k,表示最多能进行 k 次交易(一次买入和一次卖出为一次交易),问最终能获得的最大利润
算法和思路
这题不会做,是直接去看题解的
动态规划
与其余的股票问题类似,我们使用一系列变量存储「买入」的状态,再用一系列变量存储「卖出」的状态,通过动态规划的方法即可解决本题
我们用 buy[i][j] 表示对于数组 prices[0..i] 中的价格而言,进行恰好 j 笔交易,并且当前手上持有一支股票,这种情况下的最大利润;用 sell[i][j] 表示恰好进行 j 笔交易,并且当前手上不持有股票,这种情况下的最大利润
那么我们可以对状态转移方程进行推导。对于 buy[i][j],我们考虑当前手上持有的股票是否是在第 i 天买入的。如果是第 i 天买入的,那么在第 i−1 天时,我们手上不持有股票,对应状态 sell[i−1][j],并且需要扣除 prices[i] 的买入花费;如果不是第 i 天买入的,那么在第 i−1 天时,我们手上持有股票,对应状态 buy[i][j]。那么我们可以得到状态转移方程
同理对于 sell[i][j],如果是第 i 天卖出的,那么在第 i−1 天时,我们手上持有股票,对应状态 buy[i−1][j−1],并且需要增加 prices[i] 的卖出收益;如果不是第 i 天卖出的,那么在第 i−1 天时,我们手上不持有股票,对应状态 sell[i−1][j]。那么我们可以得到状态转移方程:
由于在所有的 n 天结束后,手上不持有股票对应的最大利润一定是严格由于手上持有股票对应的最大利润的,然而完成的交易数并不是越多越好(例如数组 prices 单调递减,我们不进行任何交易才是最优的),因此最终的答案即为 sell[n−1][0..k] 中的最大值
细节
在上述的状态转移方程中,确定边界条件是非常重要的步骤。我们可以考虑将所有的 buy[0][0..k] 以及 sell[0][0..k] 设置为边界
对于 buy[0][0..k],由于只有 prices[0] 唯一的股价,因此我们不可能进行过任何交易,那么我们可以将所有的 buy[0][1..k] 设置为一个非常小的值,表示不合法的状态。而对于 buy[0][0],它的值为 −prices[0],即「我们在第 0 天以 prices[0] 的价格买入股票」是唯一满足手上持有股票的方法
对于 sell[0][0..k],同理我们可以将所有的 sell[0][1..k] 设置为一个非常小的值,表示不合法的状态。而对于 sell[0][0],它的值为 0,即「我们在第 0 天不做任何事」是唯一满足手上不持有股票的方法
在设置完边界后,我们就可以使用二重循环对状态进行转移。需要注意的是,sell[i][j] 的状态转移方程中包含 buy[i−1][j−1],在 j = 0 时其表示不合法的状态,因此在 j = 0 时,我们无需对 sell[i][j] 进行转移,让其保持值为 0 即可
最后需要注意的是,因为 n 天最多只能进行 n / 2 笔交易,因此我们可以从 k 和 n / 2 中取较小值对 k 重新赋值之后再进行动态规划
算法源码
动态规划
1 | class Solution { |