LeetCode每日一题,85. Maximal Rectangle
先看题目描述
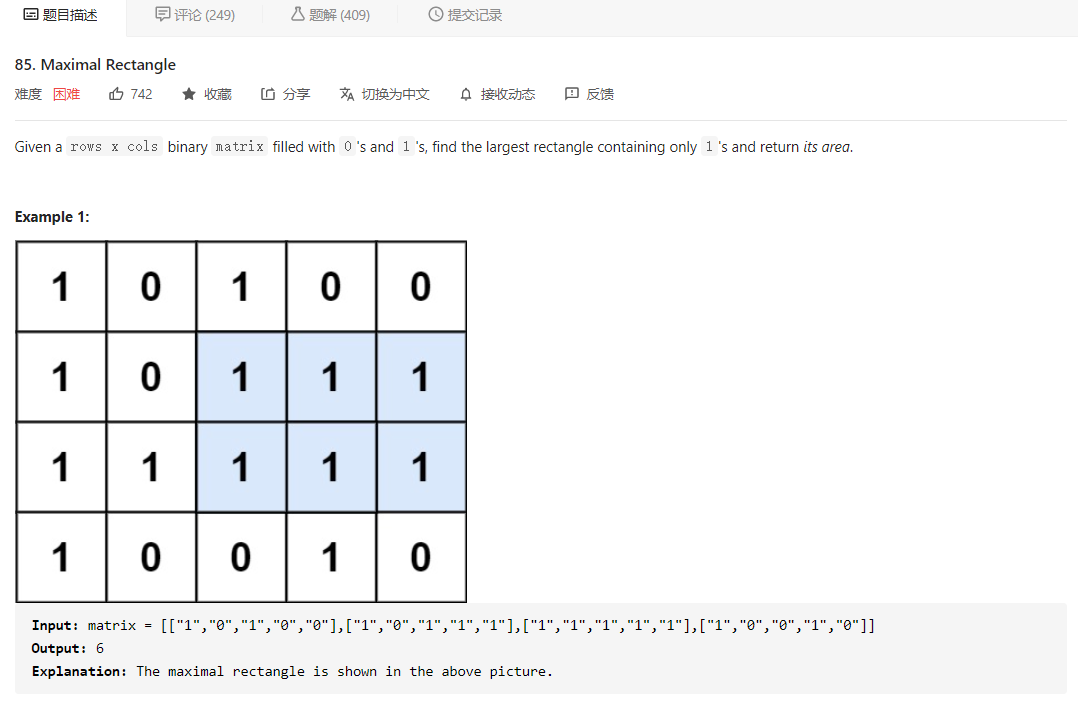
大意就是给定一个只包含 0 和 1 的二维矩阵,让我们找出只包含 1 的最大矩阵,并返回其面积
算法和思路
这题不会,看了题解才做出来的
使用柱状图的优化暴力算法
我们首先计算出矩阵的每个元素的左边连续 1 的数量,使用二维数组 left 记录,其中 left[i][j] 为矩阵第 i 行第 j 列元素的左边连续 1 的数量
随后,对于矩阵中任意一个点,我们枚举以该点为右下角的全 1 矩形。具体而言,当考察以 matrx[i][j] 为右下角的矩形时,我们枚举 0 <= k <= i 的所有可能的 k,此时矩阵的最大宽度为 left[i][j],left[i - 1][j],…,left[k][j] 中的最小值。对于每个点重复这一过程,就可以得到全局的最大矩形,最后返回面积即可
我们预计算最大宽度的方法事实上将输入转化成了一系列的柱状图,我们针对每个柱状图计算最大面积
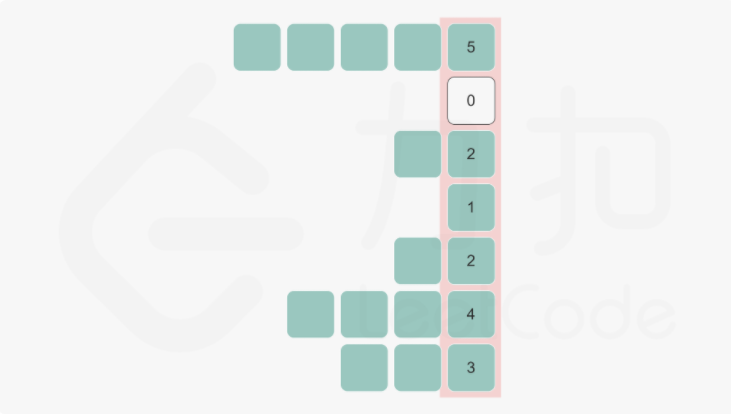
单调栈
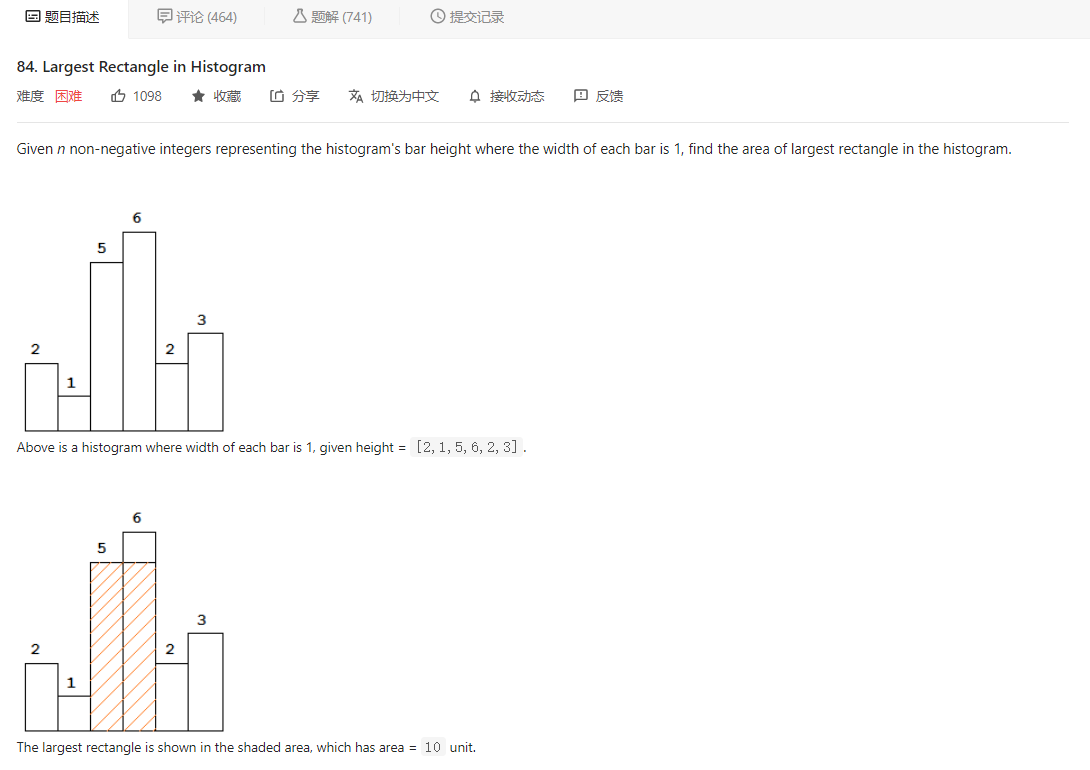
这个解法很大程度上参照了 leetcode 的第 84 题,柱状图中的最大矩形
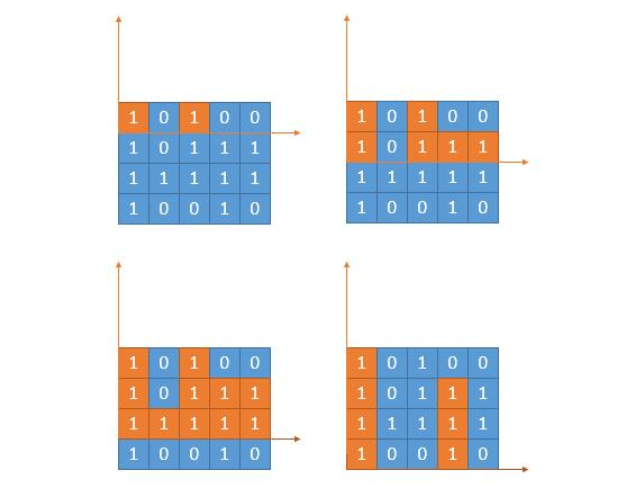
做了 84 题后,再回头看这道题,看下面的橙色部分,会发现完全就是一道题
于是我们只需从上到下逐层的计算 heights 数组,并利用 heights 数组调用第 84 题的单调栈解法就可以,用一个变量 max 来维护全 1 矩形的最大面积,最后返回 max 即可
算法源码
使用柱状图的优化暴力算法
1 | class Solution { |
单调栈
1 | class Solution { |