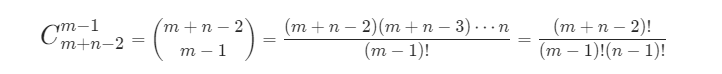LeetCode每日一题,922. Sort Array By Parity II
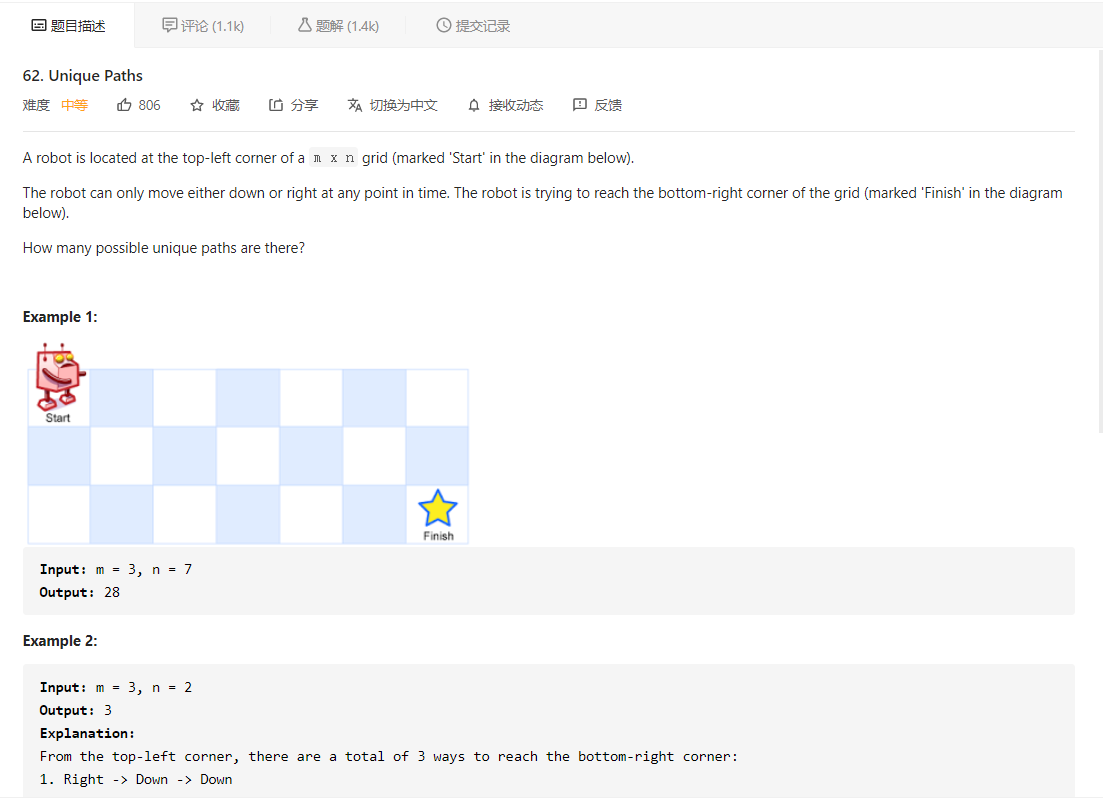
先看题目描述
大意就是给定一个 m × n 的矩阵,一个机器人只能向右走或向下走,问从左上角走到右下角共有多少条路径
算法和思路
动态规划
我们用 f[i, j] 表示从左上角走到 [i, j] 的路径数量,其中 i 和 j 的范围分别是 [0, m) 和 [0, n)
由于规定机器人只能向右走或向下走,那么机器人走到 [i, j] 经过的前一个格子是 [i -1, j] 或 [i, j - 1]
状态转移方程为:f[i, j] = f[i - 1, j] + f[i, j - 1],最后返回 f[m - 1, n - 1] 即可
数学组合
这题最开始想到的是用排列组合来做,在一个 m × n 的矩阵里,从左上角走到右下角,一共需要走 m+ n - 2 步,其中要往下走 m - 1 步,往右走 n - 1 步。那么问题就转化成了 m + n - 2 次的总移动里选 m - 1 次往下移动的方案数,就变成了数学中的排列组合问题
组合数如下图所示
算法源码
动态规划
1 | class Solution { |
数学组合
1 | class Solution { |
下面是题解的实现这个算法的源码,感觉题解的这个代码要更巧妙些
1 | class Solution { |