分割数组为连续子序列

LeetCode每日一题，659. Split Array into Consecutive Subsequences

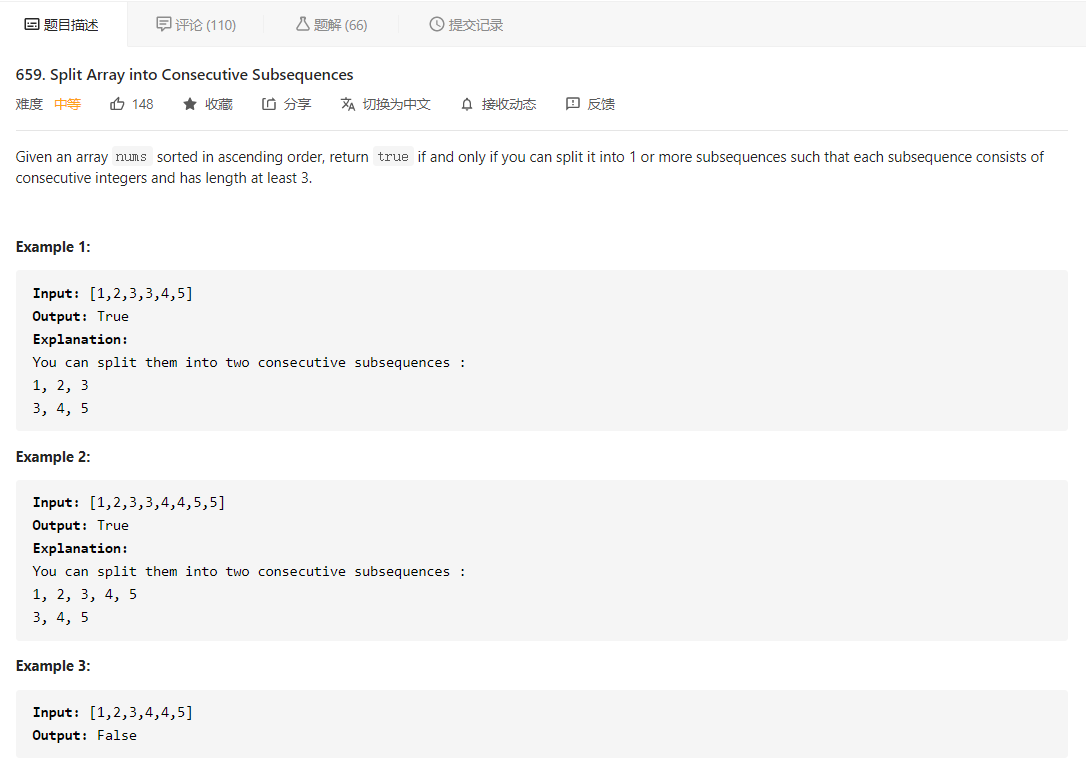
先看题目描述

大意就是给定一个升序排列的数组，问能否把该数组分割为连续的子序列，要求分割出的子序列的长度至少为 3

算法思路

这题不会做，看题解以后才做出来的

哈希表+最小堆

由于需要将数组分割成一个或多个由连续整数组成的子序列，因此只要知道子序列的最后一个数字和子序列的长度，就能确定子序列

当 x 在数组中时，如果存在一个子序列以 x−1 结尾，长度为 k，则可以将 x 加入该子序列中，得到长度为 k+1 的子序列。如果不存在以 x−1 结尾的子序列，则必须新建一个只包含 x 的子序列，长度为 1

当 x 在数组中时，如果存在多个子序列以 x−1 结尾，应该将 x 加入其中的哪一个子序列？由于题目要求每个子序列的长度至少为 3，显然应该让最短的子序列尽可能长，因此应该将 x 加入其中最短的子序列

基于上述分析，可以使用哈希表和最小堆进行实现

哈希表的 key 为子序列的最后一个数字，value 为一个最小堆，用于存储所有的子序列长度，最小堆满足堆顶的元素是最小的，因此堆顶的元素即为最短的子序列长度

遍历数组，当遍历到元素 x 时，可以得到一个以 x 结尾的子序列

如果哈希表中存在以 x−1 结尾的子序列，则取出以 x−1 结尾的最小的子序列长度，将子序列长度加 1 之后作为以 x 结尾的子序列长度。此时，以 x−1 结尾的子序列减少了一个，以 x 结尾的子序列增加了一个
如果哈希表中不存在以 x−1 结尾的子序列，则新建一个长度为 1 的以 x 结尾的子序列

由于数组是有序的，因此当遍历到元素 x 时，数组中所有小于 x 的元素都已经被遍历过，不会出现当前元素比之前的元素小的情况

遍历结束之后，检查哈希表中存储的每个子序列的长度是否都不小于 3，即可判断是否可以完成分割。由于哈希表中的每条记录的值都是最小堆，堆顶元素为最短的子序列长度（以当前的键为最后一个数字的子序列），因此只要遍历每个最小堆的堆顶元素，即可判断每个子序列的长度是否都不小于 3

贪心

从方法一可以看到，对于数组中的元素 x，如果存在一个子序列以 x−1 结尾，则可以将 x 加入该子序列中。将 x 加入已有的子序列总是比新建一个只包含 x 的子序列更优，因为前者可以将一个已有的子序列的长度增加 1，而后者新建一个长度为 1 的子序列，而题目要求分割成的子序列的长度都不小于 3，因此应该尽量避免新建短的子序列

基于此，可以通过贪心的方法判断是否可以完成分割

使用两个哈希表，第一个哈希表存储数组中的每个数字的剩余次数，第二个哈希表存储数组中的每个数字作为结尾的子序列的数量

初始时，每个数字的剩余次数即为每个数字在数组中出现的次数，因此遍历数组，初始化第一个哈希表

在初始化第一个哈希表之后，遍历数组，更新两个哈希表。只有当一个数字的剩余次数大于 0 时，才需要考虑这个数字是否属于某个子序列。假设当前元素是 x，进行如下操作

首先判断是否存在以 x-1 结尾的子序列，即根据第二个哈希表判断 x−1 作为结尾的子序列的数量是否大于 0，如果大于 0，则将元素 x 加入该子序列中。由于 x 被使用了一次，因此需要在第一个哈希表中将 x 的剩余次数减 1。又由于该子序列的最后一个数字从 x-1 变成了 x，因此需要在第二个哈希表中将 x-1 作为结尾的子序列的数量减 1，以及将 x 作为结尾的子序列的数量加 1
否则，x 为一个子序列的第一个数，为了得到长度至少为 3 的子序列，x+1 和 x+2 必须在子序列中，因此需要判断在第一个哈希表中 x+1 和 x+2 的剩余次数是否都大于 0
- 当 x+1 和 x+2 的剩余次数都大于 0 时，可以新建一个长度为 3 的子序列 [x, x+1, x+2]。由于这三个数都被使用了一次，因此需要在第一个哈希表中将这三个数的剩余次数分别减 1。又由于该子序列的最后一个数字是 x+2，因此需要在第二个哈希表中将 x+2 作为结尾的子序列的数量加 1
- 否则，无法得到长度为 33 的子序列 [x,x+1,x+2]，因此无法完成分割，返回 false

如果整个数组遍历结束时，没有遇到无法完成分割的情况，则可以完成分割，返回 true

算法源码

哈希表+最小堆

这个代码中对于哈希表的 entrySet 键值对的使用方法值得学习，还有这里的最小堆是使用 Java 中的优先级队列实现的，不重写 Comparator 时就默认升序排列

import java.util.*;

class Solution {
    public boolean isPossible(int[] nums) {
        Map<Integer, PriorityQueue<Integer>> map = new HashMap<>();
        for (int num : nums) {
            if (!map.containsKey(num)) {
                map.put(num, new PriorityQueue<>());
            }
            if (map.containsKey(num - 1)) {
                int prevLength = map.get(num - 1).poll();
                if (map.get(num - 1).isEmpty()) {
                    map.remove(num - 1);
                }
                map.get(num).offer(prevLength + 1);
            } else {
                map.get(num).offer(1);
            }
        }
        for (Map.Entry<Integer, PriorityQueue<Integer>> entry : map.entrySet()) {
            if (entry.getValue().peek() < 3) {
                return false;
            }
        }
        return true;
    }
}

贪心

下面这个是看着题解实现的代码，使用了两个哈希表来存储，注意 endMap 中存储的是数组中每个数字作为结尾的长度大于等于 3 的子序列的数量

import java.util.*;

class Solution {
    public boolean isPossible(int[] nums) {
        Map<Integer, Integer> countMap = new HashMap<>();
        Map<Integer, Integer> endMap = new HashMap<>();
        for (int num : nums) {
            countMap.put(num, countMap.getOrDefault(num, 0) + 1);
        }
        for (int num : nums) {
            int count = countMap.get(num);
            if (count > 0) {
                countMap.put(num, count - 1);
                int prevCount = endMap.getOrDefault(num - 1, 0);
                if (prevCount > 0) {
                    endMap.put(num - 1, prevCount - 1);
                    endMap.put(num, endMap.getOrDefault(num, 0) + 1);
                } else {
                    int count1 = countMap.getOrDefault(num + 1, 0);
                    int count2 = countMap.getOrDefault(num + 2, 0);
                    if (count1 > 0 && count2 > 0) {
                        countMap.put(num + 1, count1 - 1);
                        countMap.put(num + 2, count2 - 1);
                        endMap.put(num + 2, endMap.getOrDefault(num + 2, 0) + 1);
                    } else {
                        return false;
                    }
                }
            }
        }
        return true;
    }
}

因为使用哈希表来存取数据的操作比较耗时，而题目中又限定了数组的长度小于等于 10000，于是我用两个数组代替了两个哈希表来存储数组中的每个数字的剩余次数和数组中每个数字作为结尾的长度大于等于 3 的子序列的数量，极大地提高了代码的运行速度

import java.util.*;

class Solution {
    public boolean isPossible(int[] nums) {
        int min = nums[0];
        int len = nums[nums.length - 1] - min + 1;
        int[] counts = new int[len];
        int[] ends = new int[len];
        for (int num : nums) {
            counts[num - min]++;
        }
        for (int num : nums) {
            int cur = num - min;
            int count = counts[cur];
            if (count > 0) {
                int prev = cur - 1;
                counts[cur]--;
                if (prev >= 0 && ends[prev] > 0) {
                    ends[prev]--;
                    ends[cur]++;
                } else {
                    int next1 = num + 1 - min;
                    int next2 = num + 2 - min;
                    int count1 = next1 < len ? counts[next1] : 0;
                    int count2 = next2 < len ? counts[next2] : 0;
                    if (count1 > 0 && count2 > 0) {
                        counts[next1]--;
                        counts[next2]--;
                        ends[next2]++;
                    } else {
                        return false;
                    }
                }
            }
        }
        return true;
    }
}