完全二叉树的节点个数

发表于
本文字数： 2k 阅读时长 ≈ 2 分钟

LeetCode每日一题，222. Count Complete Tree Nodes

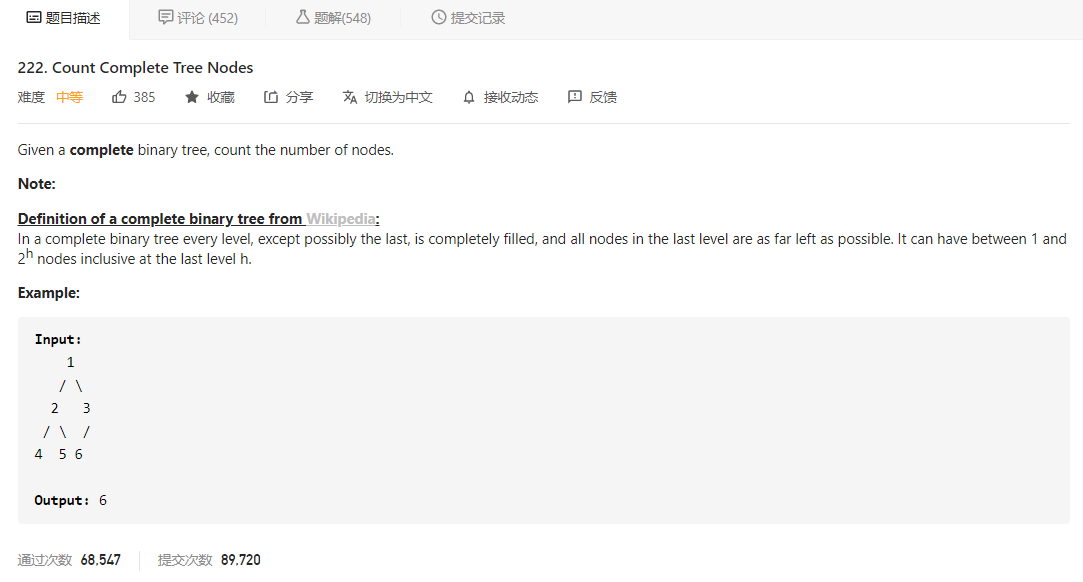
先看题目描述

DdGSBR.png

大意就是给定一棵完全二叉树，让我们计算其中的节点个数

算法和思路

自己的第一反应就是使用 dfs 或 bfs 来计算节点个数，这两个也都很容易实现，然后去看题解，发现题解给了一个很巧妙的方法

二分查找+位运算

规定根节点位于第 0 层，完全二叉树的最大层数为 h。根据完全二叉树的特性可知，完全二叉树的最左边的节点一定位于最底层，因此从根节点出发，每次访问左子节点，直到遇到叶子节点，该叶子节点即为完全二叉树的最左边的节点，经过的路径长度即为最大层数 h。若 第 h 层有一个节点，则完全二叉树的节点个数为 2^h^；若第 h 层的节点是满的，则完全二叉树的节点个数为 2^h+1^ - 1

因此对于最大层数为 h 的完全二叉树，其节点数量一定在 [2^h^, 2^h+1^ - 1] 这个范围内，可以在该范围内通过二分查找的方式得到完全二叉树的节点个数

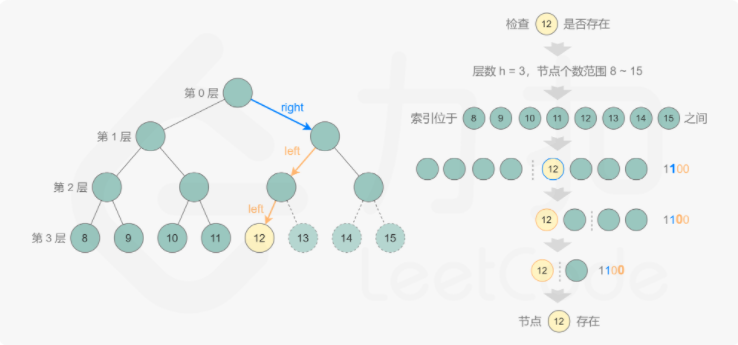
具体做法是，根据节点个数范围的上下界得到当前需要判断的节点个数 k，如果第 k 个节点存在，则节点个数一定大于或等于 k，如果第 k 个节点不存在，则节点个数一定小于 k，由此可以将查找的范围缩小一半，直到得到节点个数

如何判断第 k 个节点是否存在呢？如果第 k 个节点位于第 h 层，则 k 的二进制表示包含 h+1 位，其中最高位是 1，其余各位从高到低表示从根节点到第 k 个节点的路径，0 表示移动到左子节点，1 表示移动到右子节点。通过位运算得到第 k 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 k 个节点是否存在

DdYl6g.png

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import java.util.*;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if (root == null) return 0;
        int level = 0;
        TreeNode node = root;
        while (node.left != null) {
            node = node.left;
            level++;
        }
        int low = 1 << level;
        int high = (1 << (level + 1)) - 1;
        while (low < high) {
            int mid = low + (high - low + 1) / 2;
            if (isExitsK(root, level, mid)) {
                low = mid;
            } else {
                high = mid - 1;
            }
        }
        return low;
    }

    private boolean isExitsK(TreeNode node, int level, int mid) {
        int bits = 1 << (level - 1);
        while (bits > 0) {
            if ((bits & mid) == 0) {
                node = node.left;
            } else {
                node = node.right;
            }
            bits = bits >> 1;
        }
        return node != null;
    }
}

注意：在实现算法时有两个注意点，一是二分查找时的边界处理，二是做位运算时要注意运算符的优先级