距离顺序排列矩阵单元格

发表于
本文字数： 3.1k 阅读时长 ≈ 3 分钟

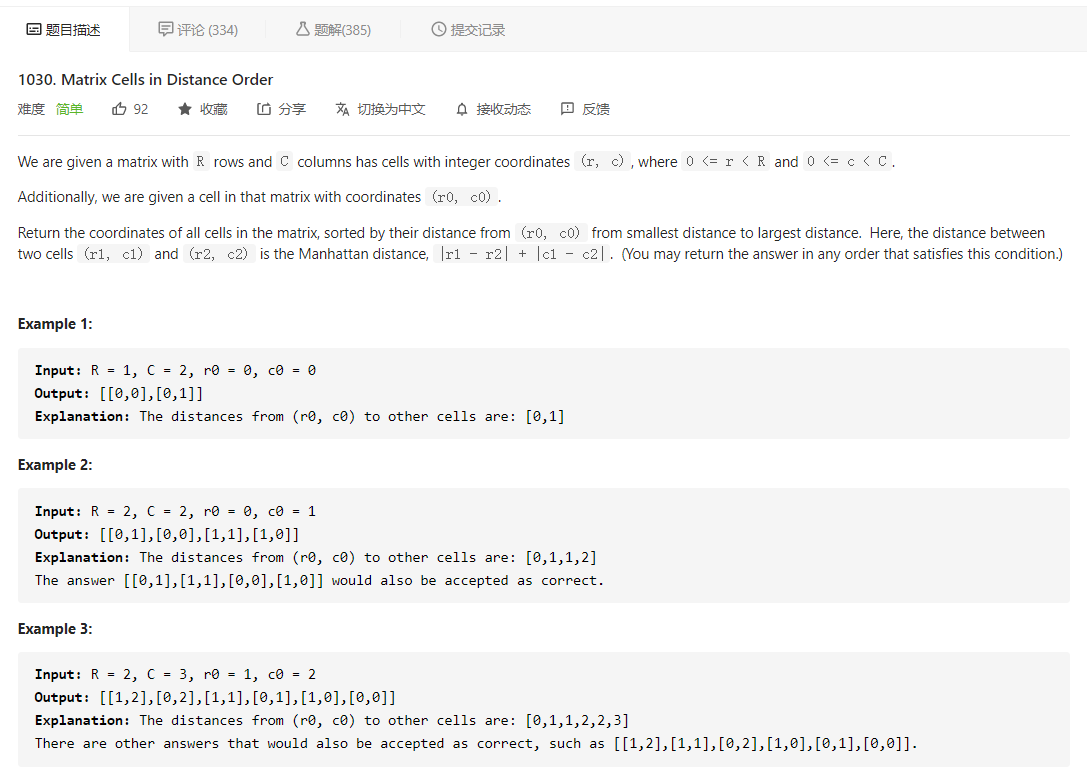
LeetCode每日一题，1030. Matrix Cells in Distance Order

先看题目描述

DmyF91.png

大意就是给定一个 R * C 的矩阵，再给定一个单元格 [r0, c0]，将矩阵中所有单元格按照距离 [r0，c0] 的曼哈顿距离进行排列，(r1, c1) 和 (r2, c2) 之间的曼哈顿距离的定义为 |r1 - r2| + |c1 - c2|

算法和思路

直接排序

思路就是先存储下矩阵内所有的点，然后重写排序规则使其按照距离 [r0, c0] 的曼哈顿距离进行排序

BFS

思路就是从 [r0, c0] 单元格开始进行广度优先搜索，然后将搜索到的单元格依次添加到结果数组中

几何法

这个是看题解才知道的方法

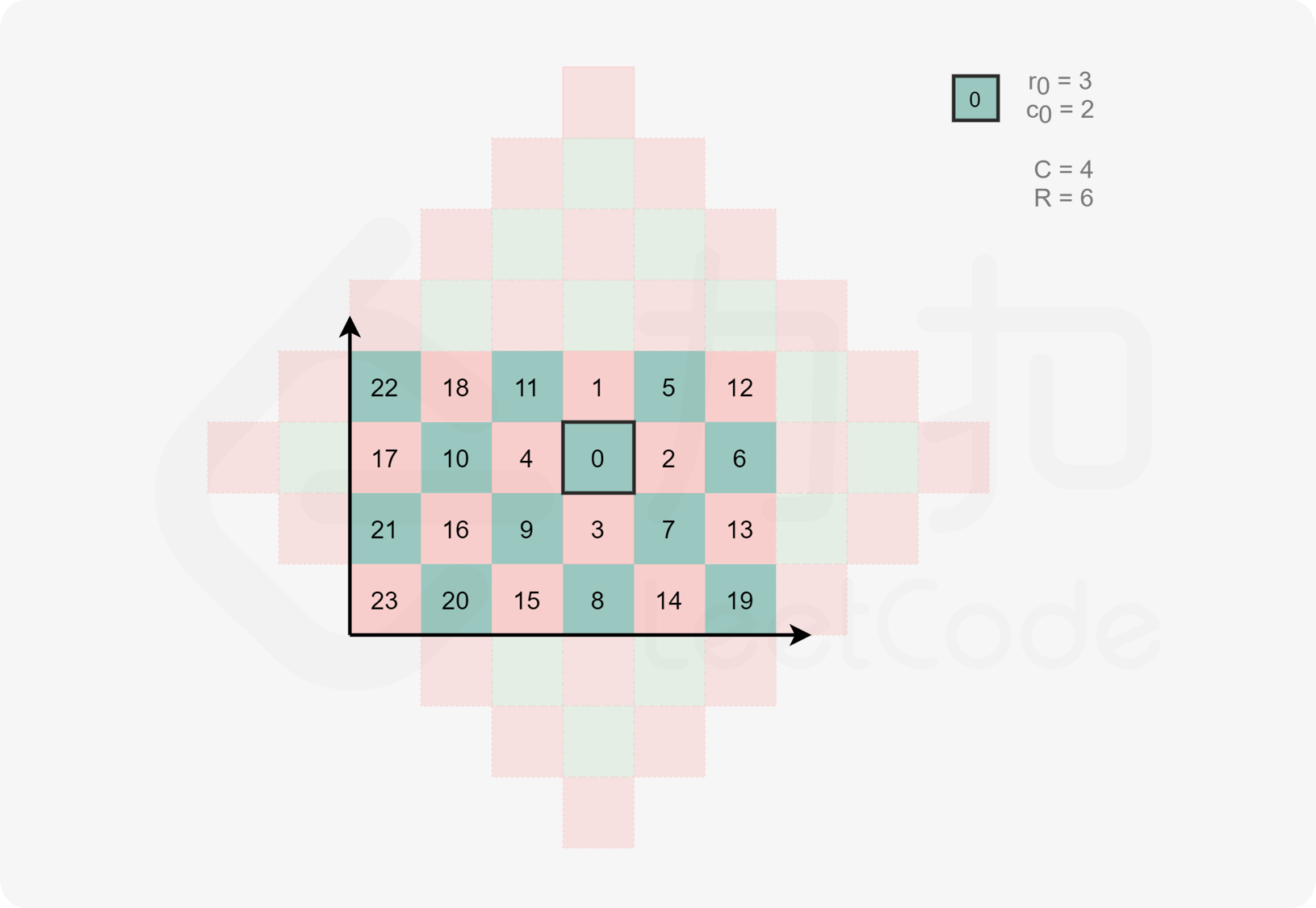
我们也可以直接变换枚举矩阵的顺序，直接按照曼哈顿距离遍历该矩形即可

注意到曼哈顿距离相同的位置恰好构成一个斜着的正方形边框，因此我们可以从小到大枚举曼哈顿距离，并使用循环来直接枚举该距离对应的边框。我们每次从该正方形边框的上顶点出发，依次经过右顶点、下顶点和左顶点，最后回到上顶点。这样即可完成当前层的遍历

算法源码

直接排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import java.util.*;

class Solution {
    public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
        int len = R * C;
        int[][] res = new int[len][];
        for (int i = 0; i < R; i++) {
            for (int j = 0; j < C; j++) {
                res[i * C + j] = new int[]{i , j};
            }
        }
        Arrays.sort(res, (a, b) -> (Math.abs(a[0] - r0) + Math.abs(a[1] - c0) - (Math.abs(b[0] - r0) + Math.abs(b[1] - c0))));
        return res;
    }
}

BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import java.util.*;

class Solution {
    public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
        int len = R * C;
        int index = 0;
        int[] dx = {1, -1, 0, 0};
        int[] dy = {0, 0, 1, -1};
        int[][] res = new int[len][];
        boolean[][] visited = new boolean[R][C];
        Deque<int[]> deque = new LinkedList<>();
        deque.add(new int[]{r0, c0});
        visited[r0][c0] = true;
        while (!deque.isEmpty()) {
            int[] cur = deque.removeFirst();
            res[index] = cur;
            index++;
            for (int i = 0; i < 4; i++) {
                int x = cur[0] + dx[i];
                int y = cur[1] + dy[i];
                if (x >= 0 && x < R && y >= 0 && y < C && !visited[x][y]) {
                    deque.add(new int[]{x, y});
                    visited[x][y] = true;
                }
            }
        }
        return res;
    }
}

几何法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import java.util.*;

class Solution {
    public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {
        int[] dx = {1, 1, -1, -1};
        int[] dy = {1, -1, -1, 1};
        int maxDist = Math.max(r0, R - 1 - r0) + Math.max(c0, C - 1 - c0);
        int[][] res = new int[R * C][];
        res[0] = new int[]{r0, c0};
        int row = r0;
        int col = c0;
        int index = 1;
        for (int dist = 1; dist <= maxDist; dist++) {
            row--;
            for (int i = 0; i < 4; i++) {
                while (i % 2 == 0 && row != r0 || i % 2 == 1 && col != c0) {
                    if (row >= 0 && row < R && col >= 0 && col < C) {
                        res[index++] = new int[]{row, col};
                    }
                    row += dx[i];
                    col += dy[i];
                }
            }
        }
        return res;
    }
}