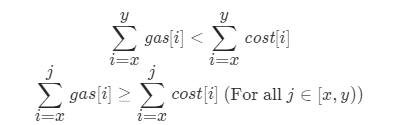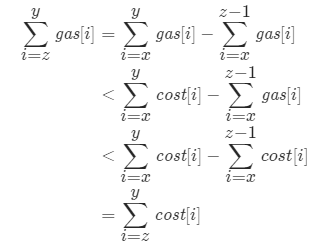加油站

发表于
本文字数： 2.4k 阅读时长 ≈ 2 分钟

LeetCode每日一题，134. Gas Station

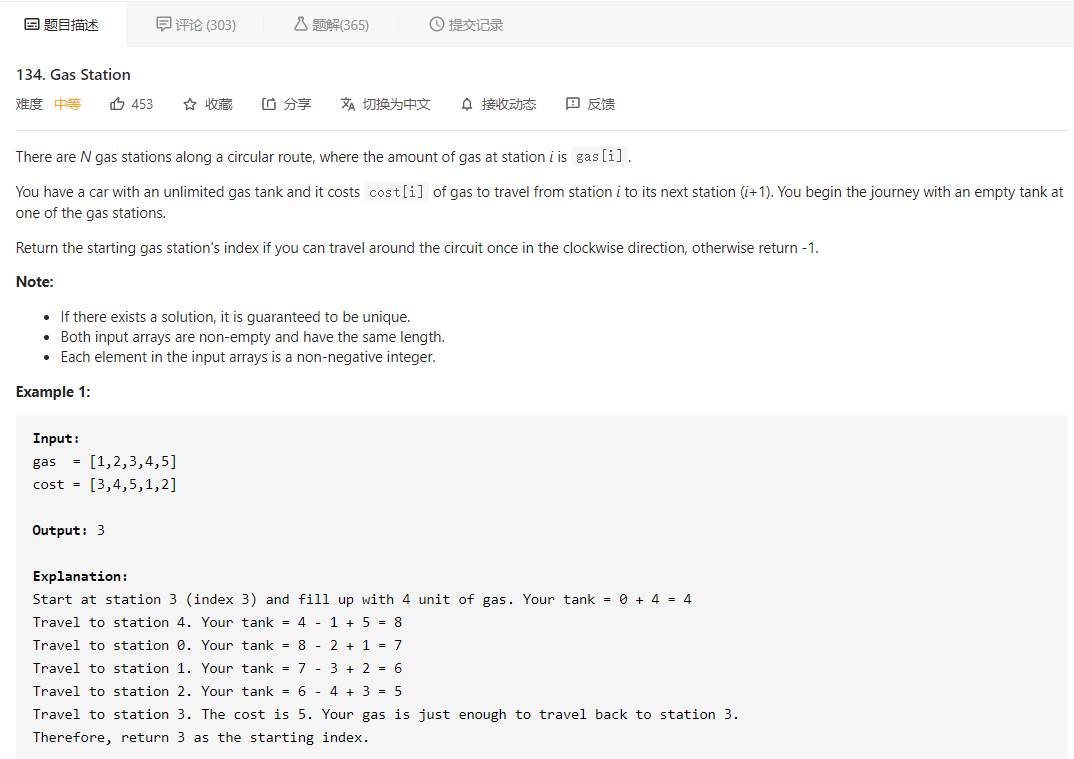
先看题目描述

DefAAS.png

大意就是给定两个数组 gas 和 cost，gas[i] 代表第 i 个加油站可以给车加的油，cost[i] 代表从第 i 个加油站走到第 i + 1 个加油站，需要消耗多少油，起始时车里没油，问从某个加油站开始走，每到一个加油站就加油，能否走一个循环，不能的话就返回 -1，能的话就返回起点加油站的位置

算法和思路

暴力法

第一想法就是暴力遍历，遍历每个加油站，判断从该加油站开始走能否走一个循环。因为感觉这样实在是太暴力了，我就想办法优化，看到题目说若有解时该解唯一，于是想到当 gas[i - 1] - cost[i - 1] 大于等于 0 时，加油站 i 必不可能是起点，这个通过反证法可以证明，利用这点的话就不用每个加油站都判断一遍了

一次遍历

这个是看题解才明白的，要是我自己想的话估计想不出来

假设我们此前发现，从加油站 x 出发，每经过一个加油站就加一次油，第一个无法到达的加油站是 y（不妨设 x<y）。这就说明：

De4T6s.png

第一个式子表明无法到达加油站 y，第二个式子表明可以到达 y 之前的所有加油站

现在，考虑任意一个位于 x,y 之间的加油站 z，我们现在考察从该加油站出发，能否到达加油站 y，根据上面的式子，我们得到：

De5AAK.png

这就说明：从 x,y 之间的任何一个加油站出发，都无法到达加油站 y

在发现了这一个性质后，算法就很清楚了：我们首先检查第 0 个加油站，并试图找到第一个无法到达的加油站 x；如果能找到，下一次就从加油站 x+1 开始检查。最终，我们只遍历了原数组一次

算法源码

暴力法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int len = gas.length;
        if (len < 1) return -1;
        int[] rest = new int[len];
        int sum = 0;
        for (int i = 0; i < len; i++) {
            rest[i] = gas[i] - cost[i];
            sum += rest[i];
        }
        if (sum < 0) return -1;
        if (len == 1) return 0;
        if (rest[len - 1] < 0) {
            int temp = 0;
            int i = 0;
            for (; i < len; i++) {
                temp += rest[i];
                if (temp < 0) break;
            }
            if (i == len) return 0;
        }
        for (int i = 1; i < len; i++) {
            if (rest[i - 1] >= 0) {
                continue;
            }
            int temp = 0;
            int index = i;
            int j = 0;
            for (; j < len; j++) {
                temp += rest[(index + j) % len];
                if (temp < 0) break;
            }
            if (j == len) return i;
        }
        return -1;
    }
}

一次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int len = gas.length;
        int start = 0;
        int curGas = 0;
        int totalGas = 0;
        for (int i = 0; i < len; i++) {
            curGas += gas[i] - cost[i];
            totalGas += gas[i] - cost[i];
            if (curGas < 0) {
                start = i + 1;
                curGas = 0;
            }
        }
        return totalGas >= 0 ? start : -1;
    }
}

这就是一次遍历的代码，对于最后的返回值，应该是用到了一个性质：当 totalGas >= 0时，题目要求的起点加油站一定存在，但这个性质我并不知道如何证明；当toalGas < 0 时，一定无解这点倒是很好理解的