根据身高重建队列

LeetCode每日一题，406. Queue Reconstruction by Height

先看题目描述

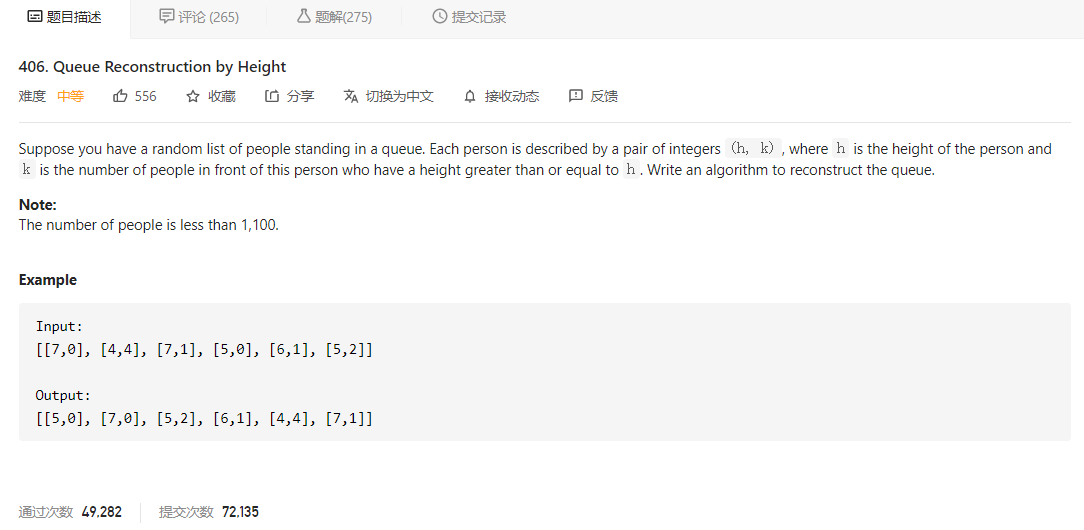
大意就是给定一个数组，每个整数对 (h, k) 代表一个人，h 代表身高，k 代表排在这个人前面且身高大于等于 h 的人数，让我们编写算法来重建队列

算法和思路

从低到高排

我们首先得将原数组按照 h 为第一关键字升序排列，k 为第二关键字降序排列，如果我们按照排完序后的顺序，依次将每个人放入队列中，那么当我们放入第 i个人时：

第 0,⋯,i−1 个人已经在队列中被安排了位置，并且他们无论站在哪里，对第 i 个人都没有任何影响，因为他们都比第 i 个人矮；
而第 i+1,⋯,n−1 个人还没有被放入队列中，但他们只要站在第 i 个人的前面，就会对第 i 个人产生影响，因为他们都比第 i 个人高

如果我们在初始时建立一个包含 n 个位置的空队列，而我们每次将一个人放入队列中时，会将一个「空」位置变成「满」位置，那么当我们放入第 i 个人时，我们需要给他安排一个「空」位置，并且这个「空」位置前面恰好还有 Ki 个「空」位置，用来安排给后面身高更高的人。也就是说，第 i 个人的位置，就是队列中从左往右数第 Ki + 1 个空位置

从高到低排

同样地，我们也可以对原数组按照 h 为第一关键字降序排列，k 为第二关键字升序排列，如果我们按照排完序后的顺序，依次将每个人放入队列中，那么当我们放入第 i个人时

第 0,⋯,i−1 个人已经在队列中被安排了位置，他们只要站在第 i 个人的前面，就会对第 i 个人产生影响，因为他们都比第 i 个人高；
而第 i+1,⋯,n−1 个人还没有被放入队列中，并且他们无论站在哪里，都不会对第 i 个人产生影响，因为他们都比第 i 个人矮

后面的人既然不会对第 i 个人造成影响，我们可以采用「插空」的方法，依次给每一个人在当前的队列中选择一个插入的位置。也就是说，当我们放入第 i 个人时，只需要将其插入队列中，使得他的前面恰好有 Ki 个人即可

我感觉这两种解法的主要区别可以这样理解：对于放入的第 i 个人，我们只需要关注比他高的人，因为矮与他的人不会对其造成影响。所以从低到高排时关注的是要给比他高的人在前面留多少个空；而从高到低排时关注的是他前面应该有多少人

算法和源码

从低到高排

import java.util.*;

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        int len = people.length;
        boolean[] used = new boolean[len];
        int[][] ans = new int[len][2];
        Arrays.sort(people, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0];
            }
        });
        for (int i = 0; i < len; i++) {
            int index = 0;
            while (used[index]) {
                index++;
            }
            int offset = people[i][1];
            for (int j = 0; j < offset; j++) {
                index++;
                while (used[index]) {
                    index++;
                }
            }
            ans[index] = people[i];
            used[index] = true;
        }
        return ans;
    }
}

上面这个是自己写的，下面这个是题解的写法，效率稍微高点。这里可以使用 ans[i] == null 是因为初始化 ans 数组时没指定第二维的长度，若指定了第二维的长度，就不能这样用了

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        Arrays.sort(people, new Comparator<int[]>() {
            public int compare(int[] person1, int[] person2) {
                if (person1[0] != person2[0]) {
                    return person1[0] - person2[0];
                } else {
                    return person2[1] - person1[1];
                }
            }
        });
        int n = people.length;
        int[][] ans = new int[n][];
        for (int[] person : people) {
            int spaces = person[1] + 1;
            for (int i = 0; i < n; ++i) {
                if (ans[i] == null) {
                    --spaces;
                    if (spaces == 0) {
                        ans[i] = person;
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

从高到低排

import java.util.*;

class Solution {
    public int[][] reconstructQueue(int[][] people) {
        int len = people.length;
        List<int[]> ans = new ArrayList<>();
        Arrays.sort(people, (a,b)->(a[0] == b[0] ? a[1] - b[1] : b[0] - a[0]));
        for (int[] tmp : people) {
            ans.add(tmp[1], tmp);
        }
        return ans.toArray(new int[len][2]);
    }
}

注意：这里的重写数组排序规则的写法和之前有不同，这是看运行效率高的代码学习到的写法，经测试发现这种写法会比之前那种重写排序规则的写法运行效率更高，但感觉可读性是比之前那个写法略差点的，还有最后这个列表转数组的写法也值得学习