移掉k位数字

发表于
本文字数： 5.4k 阅读时长 ≈ 5 分钟

LeetCode每日一题，402. Remove K Digits

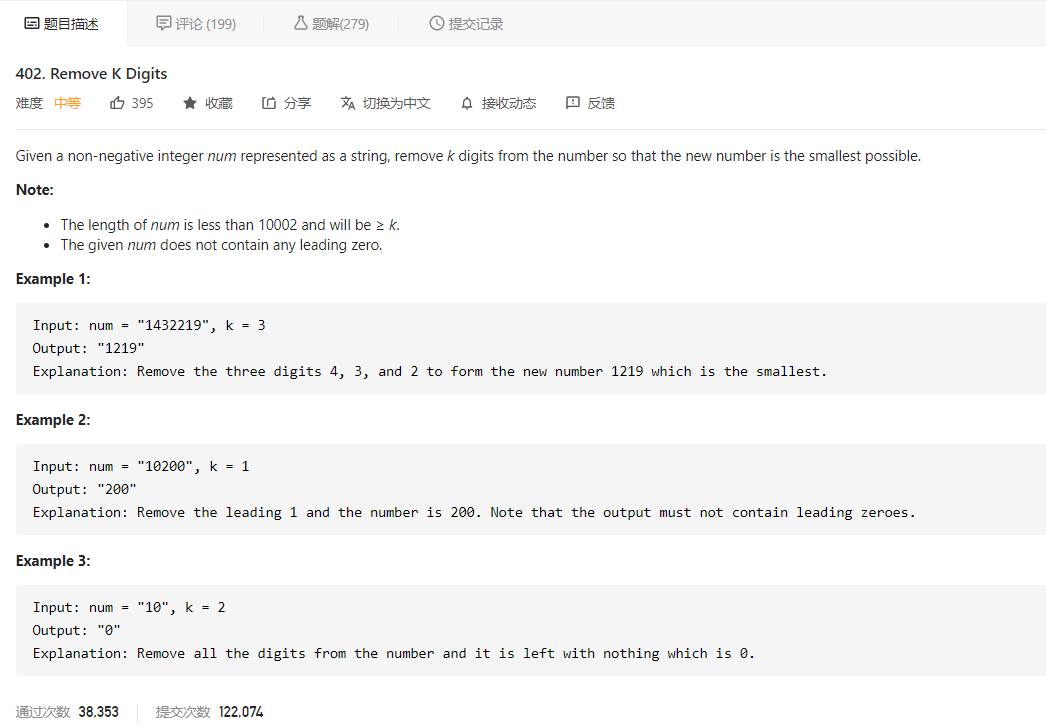
先看题目描述

DFMlMd.png

大意就是给定一个字符串表示的整数，再给定一个 k，代表我们要移除整数中的 k 个数字，使剩下的数字最小，并将其返回

算法和思路

自己一开始的想法是题目要求删除 k 个数字，使剩下数字最小，就等价于用原来整数中的 len- k 个数字组合成一个新数字，使这个新数字最小。

以第一个例子 1432219 为例，k = 3， len = 7，我们需要选出四个数，将其按顺序组合成新数字，使新数字最小。那么我们先选出第一个数字，该数字只能在下标 [0, 3] 范围内的数选择，选择该范围内最小的数 1；由于 1 的下标为 0，第二个数字只能在下标 [1, 4] 范围内的数选择，选择该范围内最小的数 2(该范围内有两个 2，选择下标较小的那个)；2 的下标为 3，第三个数字在下标 [4, 5] 范围内的数选择，选择其中最小的数 1；1 的下标为 5，最后一个数字只能在下标为 [6, 6] 范围内的数选择，选择了 9。于是最后返回 “1219”

具体到实现上，为了提高运行速度，我们需要用数组预先把字符串中的数字都存储起来

算法流程

  • 初始化 index = -1，flag = false，len = len(num)，res= “”，数组 nums 存储字符串 num 中的所有数字
  • 当 k < len时，执行循环：
    • 遍历下标为 [index + 1, k] 之间的数，找出其中最小的数 min 及其对应下标 min_index
    • 将 min 添加到 res 最后
    • 更新 index = min_index， k = k + 1

注意：在具体实现时还要注意，在每次添加 min 到 res 最后时，要注意对开头的 0 进行处理

贪心+单调栈

这个解法是看题解才想通的

对于两个相同长度的数字序列，最左边不同的数字决定了这两个数字的大小，例如，对于 A = 1axxx，B = 1bxxx，如果 a>b 则 A > B

基于此，我们可以知道，若要使得剩下的数字最小，需要保证靠前的数字尽可能小

贪心策略：给定一个长度为 n 的数字序列 num，从左往右找到第一个位置 i（i>0）使得 num[i] < num[i - 1]，并删去 num[i - 1]；如果不存在，说明整个数字序列单调不降，删去最后一个数字即可

基于此，我们可以每次对整个数字序列执行一次这个策略；删去一个字符后，剩下的 n−1 长度的数字序列就形成了新的子问题，可以继续使用同样的策略，直至删除 k 次

然而暴力的实现复杂度最差会达到 O(nk)（考虑整个数字序列是单调不降的），因此我们需要加速这个过程

考虑从左往右增量的构造最后的答案。我们可以用一个栈维护当前的答案序列，栈中的元素代表截止到当前位置，删除不超过 k 次个数字后，所能得到的最小整数。根据之前的讨论：在使用 k 个删除次数之前，栈中的序列从栈底到栈顶单调不降

因此，对于每个数字，如果该数字小于栈顶元素，我们就不断地弹出栈顶元素，直到

  • 栈为空
  • 或者新的栈顶元素不大于当前数字
  • 或者我们已经删除了 k 位数

上述步骤结束后我们还需要针对一些情况做额外的处理：

  • 如果我们删除了 m 个数字且 m<k，这种情况下我们需要从序列尾部删除额外的 k−m 个数字
  • 如果最终的数字序列存在前导零，我们要删去前导零
  • 如果最终数字序列为空，我们应该返回 0

最终，从栈底到栈顶的答案序列即为最小数

考虑到栈的特点是后进先出，如果通过栈实现，则需要将栈内元素依次弹出然后进行翻转才能得到最小数。为了避免翻转操作，可以使用双端队列代替栈的实现

算法源码

下面是自己实现的第一个解法的算法源码，一开始最外层用的是 while 循环，然后还是改成了 for 循环，还有需要注意的就是对前导零和最后结果只有一个 0 时等细节方面的处理。还有一点就是，将字符串 num 中的数字用一个数组存储起来，而不是每次用 num.charAt()，可以提高运行效率

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public String removeKdigits(String num, int k) {
        int len = num.length();
        if (k == len) {
            return "0";
        }
        StringBuilder res = new StringBuilder();
        int index = -1;
        int[] nums = new int[len];
        boolean flag = false;
        for (int i = 0; i < len; i++) {
            nums[i] = num.charAt(i) - '0';
        }
        for (int i = k; i < len; i++) {
            int min_index = index + 1;
            int min = nums[min_index];
            for (int j = index + 1; j <= i; j++) {
                if (nums[j] < min) {
                    min = nums[j];
                    min_index = j;
                }
            }
            index = min_index;
            if (min == 0) {
                if (flag || i == len - 1) {
                    res.append(min);
                }
            } else {
                flag = true;
                res.append(min);
            }
        }
        return res.toString();
    }
}

下面还有一个实现的该解法的源码，但我为了简化每次在目标下标范围内寻找最小数的这个过程，先重写排序规则对 nums 数组进行了排序，然后因为这个排序实在太耗时了，效率直接爆炸了，跑出来 200 多ms…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
import java.util.Arrays;
import java.util.Comparator;

class Solution {
    public String removeKdigits(String num, int k) {
        int len = num.length();
        if (k == len) {
            return "0";
        }
        StringBuilder res = new StringBuilder();
        int index = -1;
        int[][] nums = new int[len][2];
        boolean flag = false;
        for (int i = 0; i < len; i++) {
            nums[i][0] = i;
            nums[i][1] = num.charAt(i) - '0';
        }
        Arrays.sort(nums, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o1[1] == o2 [1] ? o1[0] - o2[0] : o1[1] - o2[1];
            }
        });
        while (k < len) {
            for (int[] cur : nums) {
                if (index < cur[0] && cur[0] <= k) {
                    if (cur[1] == 0) {
                        if (flag || k == len - 1) {
                            res.append(cur[1]);
                        }
                    } else {
                        flag = true;
                        res.append(cur[1]);
                    }
                    index = cur[0];
                    k++;
                    break;
                }
            }
        }
        return res.toString();
    }
}

贪心+单调栈

这个是看了题解后实现的源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import java.util.*;

class Solution {
    public String removeKdigits(String num, int k) {
        int len = num.length();
        Deque<Character> deque = new LinkedList<>();
        for (int i = 0; i < len; i++) {
            char cur = num.charAt(i);
            while (k > 0 && !deque.isEmpty() && cur < deque.peekLast()) {
                deque.removeLast();
                k--;
            }
            deque.add(cur);
        }
        if (k > 0) {
            for (int i = 0; i < k; i++) {
                deque.removeLast();
            }
        }
        StringBuilder res = new StringBuilder();
        boolean flag = true;
        while (!deque.isEmpty()) {
            char cur = deque.removeFirst();
            if (cur == '0' && flag) {
                continue;
            }
            flag = false;
            res.append(cur);
        }
        return res.length() == 0 ? "0" : res.toString();
    }
}

个人感觉这两种解法，一个是从零开始添加 len - k 个数字，使新数字最小；另一个是删除 k 个数字，使剩余数字最小。主要差别就在这个地方，最后结果显示第一个解法的效率是要更高些的，第一个解法的运行时间为 5ms，第二个为 8ms