最接近原点的k个点

LeetCode每日一题，973. K Closet Points to Origin

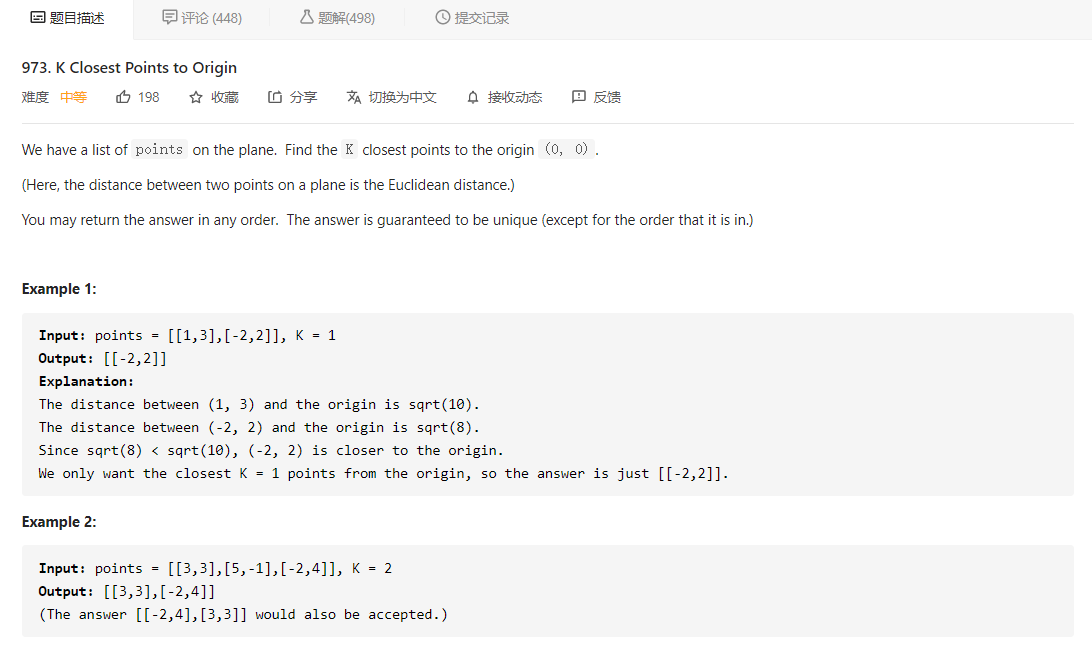
先看题目描述

大意就是给定平面上的点组成的列表，再给定一个整数 K，让我们从中找出 K 个距离原点最近的点

算法和思路

排序

大致思路就是调用 Arrays.sort() 函数，并用 new Comparator() 重写排序规则，使元素按照距离原点的距离升序排列，然后复制排序后数组的前 K 个元素并返回

优先级队列

构造一个优先级队列实时维护前 K 个最小距离的平方，在构造时用 new Comparator() 重写排序规则，使其为一个大根堆，其中元素按照距离原点距离的平方降序排列；我们将前 K 个点的编号（为了方便最后直接得到答案）以及对应的距离平方放入优先队列中，随后从第 K+1 个点开始遍历：如果当前点的距离平方比堆顶的点的距离平方要小，就把堆顶的点弹出，再插入当前的点。当遍历完成后，所有在优先队列中的点就是前 K 个距离最小的点

借助快速排序

这个实际上就是借助快排中的 partition 过程，partition 操作会将数组中的一个元素放在它最后该处于的位置上，满足其左边的元素均小于等于它，其右边的元素均大于它，若经 partition 操作后，该元素恰好处于位置 K，那么我们直接复制此时数组的前 K 个元素并返回；若在位置 K 左边，则对其右侧数组元素进行 partition 操作；若在位置 K 右边，则对其左侧数组元素继续进行 partiton 操作，直至经 partition 操作后某个元素处于位置 K

算法源码

排序

import java.util.*;

class Solution {
    public int[][] kClosest(int[][] points, int K) {
        Arrays.sort(points, new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return (o1[0] * o1[0] + o1[1] * o1[1]) - (o2[0] * o2[0] + o2[1] * o2[1]);
            }
        });
        return Arrays.copyOfRange(points, 0, K);
    }
}

优先级队列

import java.util.*;

class Solution {
    public int[][] kClosest(int[][] points, int K) {
        int[][] res = new int[K][2];
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            @Override
            public int compare(int[] o1, int[] o2) {
                return o2[0] - o1[0];
            }
        });
        for (int i = 0; i < K; i++) {
            pq.offer(new int[]{points[i][0] * points[i][0] + points[i][1] * points[i][1], i});
        }
        for (int i = K; i < points.length; i++) {
            int dist = points[i][0] * points[i][0] + points[i][1] * points[i][1];
            if (dist < pq.peek()[0]) {
                pq.poll();
                pq.offer(new int[]{dist, i});
            }
        }
        for (int i = 0; i < K; i++) {
            res[i] = points[pq.poll()[1]];
        }
        return res;
    }
}

借助快速排序的partition过程

import java.util.*;

class Solution {
    Random rand = new Random();

    public int[][] kClosest(int[][] points, int K) {
        int len = points.length;
        partition(points, 0, len - 1, K);
        return Arrays.copyOfRange(points, 0, K);
    }

    private void partition(int[][] points, int left, int right, int K) {
        int random_index = left + rand.nextInt(right - left + 1);
        swap(points, left, random_index);
        int pivot = points[left][0] * points[left][0] + points[left][1] * points[left][1];
        int lt = left;
        for (int i = left + 1; i <= right; i++) {
            int num = points[i][0] * points[i][0] + points[i][1] * points[i][1];
            if (num <= pivot) {
                lt++;
                swap(points, i, lt);
            }
        }
        swap(points, left, lt);
        if (lt < K - 1) {
            partition(points, lt + 1, right, K);
        } else if (lt > K - 1) {
            partition(points, left, lt - 1, K);
        }
    }

    private void swap(int[][] points, int i, int j) {
        int[] temp = points[i];
        points[i] = points[j];
        points[j] = temp;
    }
}