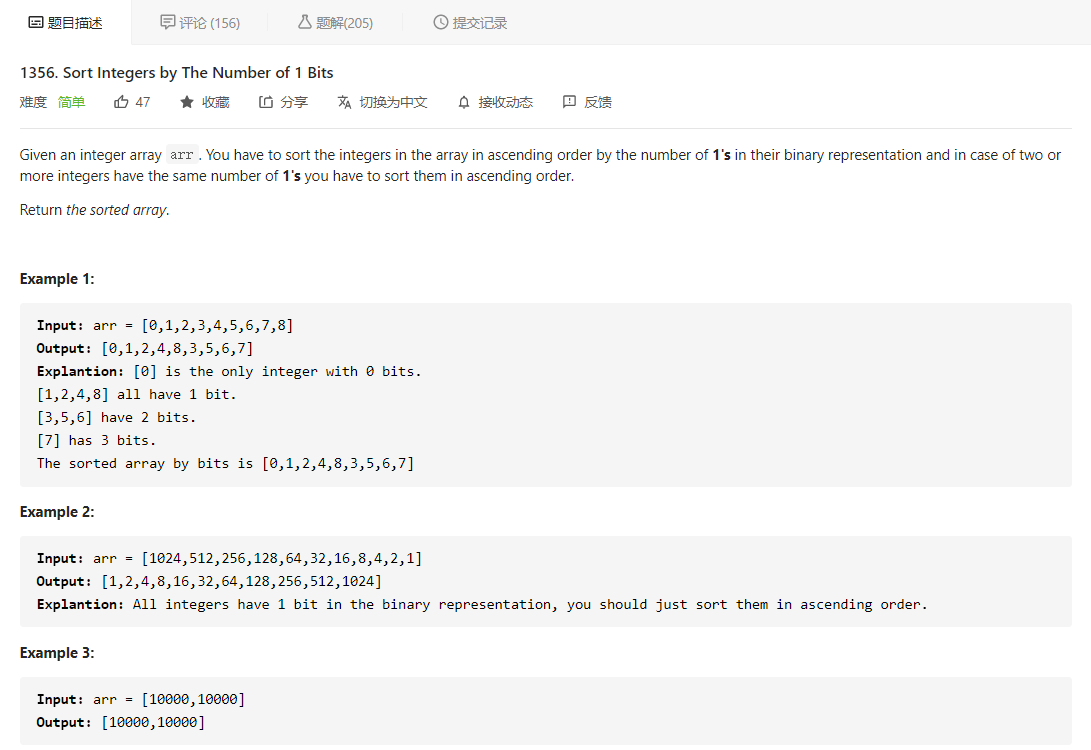
LeetCode每日一题,1356. Sort Integers by The Number of 1 Bits
先看题目描述
大意就是给定一个数组,让我们对其排序,排序规则是比较两个数的二进制表示下数字 1 的数目,小的在前面,若 1 的数目相同,则本身数值小的在前面
算法和思路
对数组的排序部分,只需调用系统自带的排序函数,然后改写下排序规则即可,那么重点就在于怎么求数字在二进制表示下数字 1 的个数
我们定义 bits[i] 为数字 i 在二进制表示下数字 1 的个数,则有如下递推式:bits[i] = bits[i >> 1] + (i & 1)
所以先线性预处理 bits 数组然后去排序即可
算法源码
1 | import java.util.*; |
这个代码中,我感觉用递推式 bits[i] = bits[i >> 1] + (i & 1) 先线性预处理 bits 数组来求数字 i 在二进制表示下数字 1 的数目很巧妙,需要注意的是 (i & 1) 外层的括号不能去掉,不然就会出问题,这个应该和运算符的优先级有关;还有就是直到现在才知道 collections.sort() 函数可以自定义排序规则,重写 Comparator 接口中的 compare 方法即可,大致就是经 compare 方法比较后,若返回值大于 0,则第一个参数放后面,否则的话第一个参数放前面,印象中 python 也有类似函数
后来又去看击败时间击败 100% 的代码,发现 java 实现了一个 Integer.bitCount() 方法,可以获取数字转化为二进制后其中数字 1 的数目,尝试去看这个方法的源码,但是并没有看懂…另外别人实现代码的这个排序方式也很巧妙,是采用赋予转化为二进制后其中数字 1 的数目和自身数值不同系数的方式来进行排序。别人一开始用的是 100000,我改成了 10001,因为题目说了数字范围为 0-10000,所以只要用个比 10000 大的数字就行。另外还发现了有趣的一点,如果采用的是 for(int num : ans) 这种 for each 循环,ans 并不会改变,应该是因为 ans[i] 这种索引的形式才会改变 ans 数组吧
1 | class Solution { |
另外 Integer.bitCount() 方法的源码如下,这个方法只可以用于 32 位的整数
1 | public static int bitCount(int i) { |