单词拆分II

LeetCode每日一题，140. WordBreakII

先看题目描述

大意就是给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子

算法和思路

• 我们先通过动态规划得到原始输入字符串的任意长度的 前缀子串 是否可以拆分为单词集合中的单词；
• 动态规划得到的数组可以帮助我们快速评估是否有解，例如 dp[i] 为 true 就代表 s[0, i - 1] 前缀子串可以被拆分为单词集合中的单词

所有任意长度的前缀是否可拆分是知道的，那么如果 后缀子串在单词集合中，这个后缀子串就是解的一部分，例如：

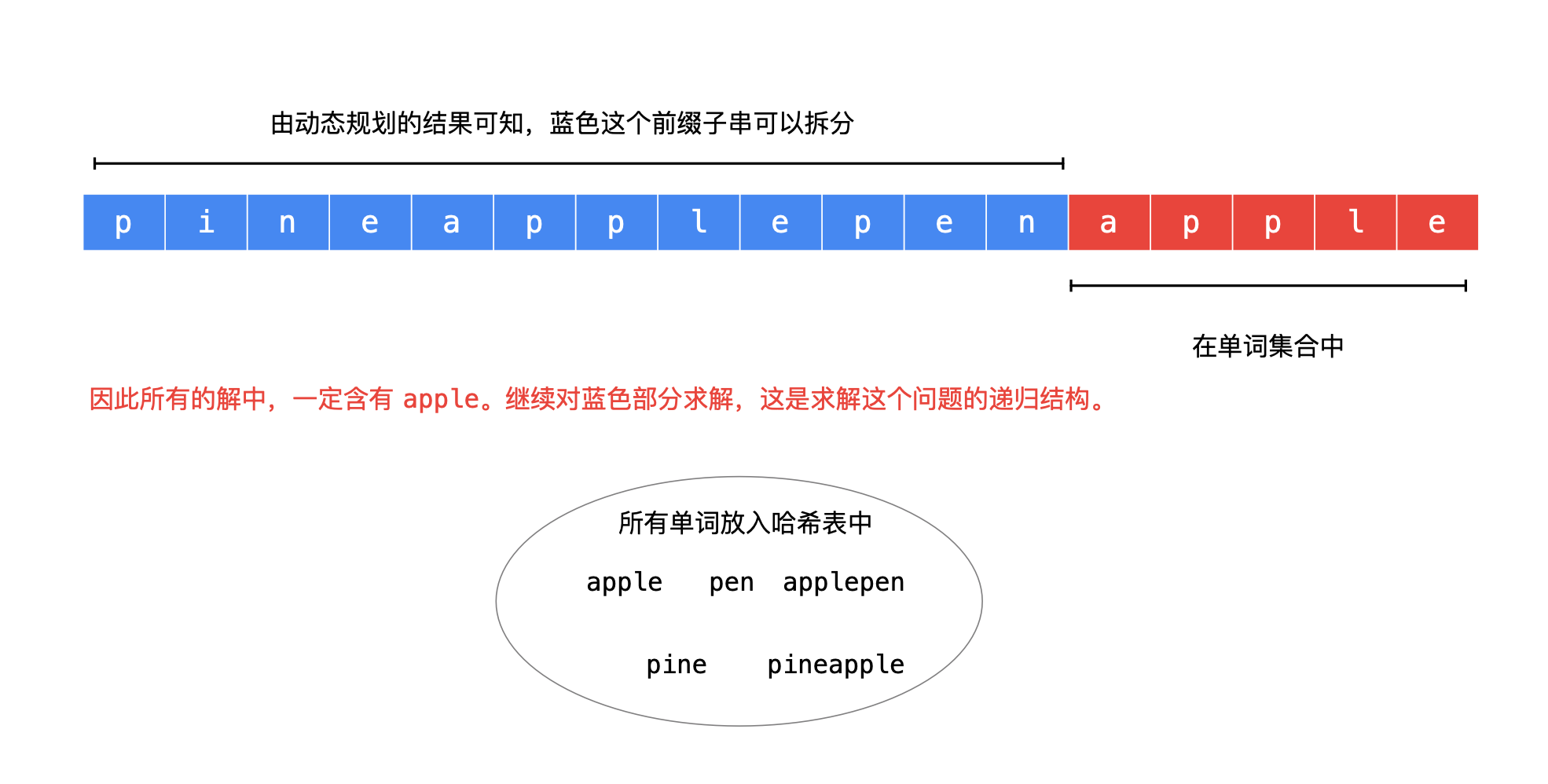
根据这个思路，可以画出树形结构如下

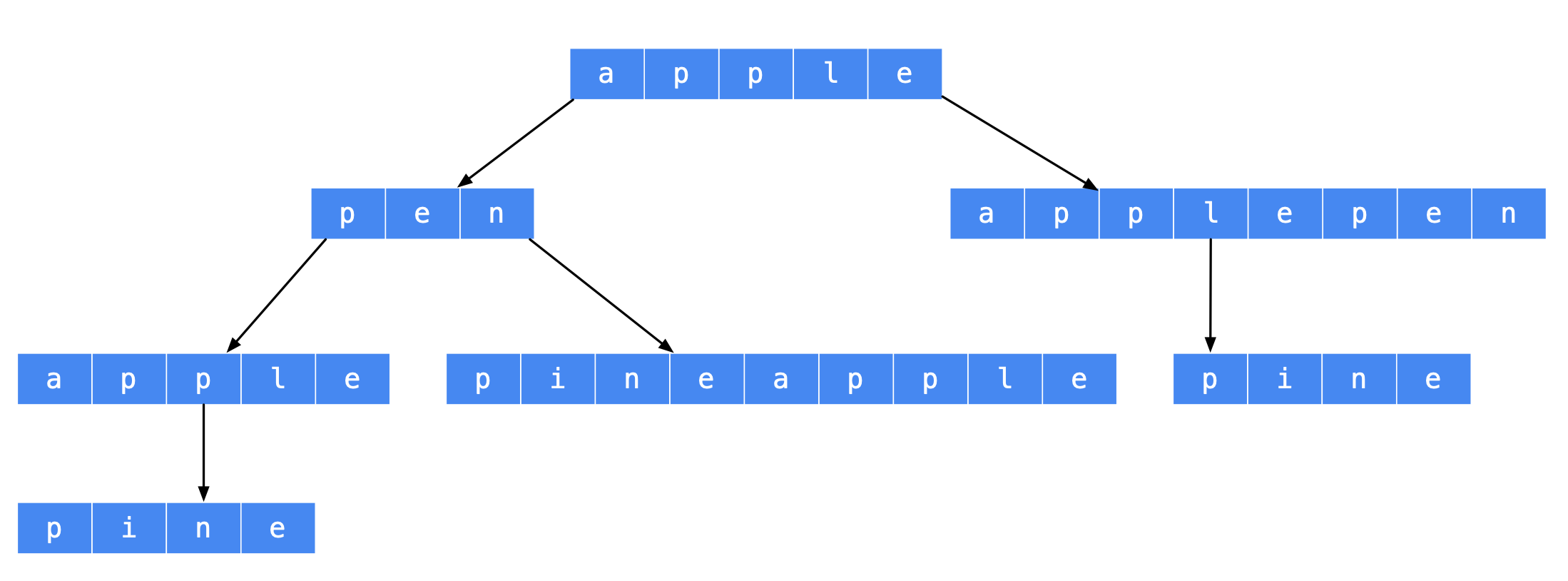
我们可以发现，树形结构中，从叶子结点到根结点的路径是符合要求的一个解，与以前做过的回溯算法的问题不一样，这个时候路径变量我们需要在依次在列表的开始位置插入元素，可以使用队列（LinkedList）实现，或者是双端队列（ArrayDeque）

算法源码

回溯+动态规划剪枝

import java.util.*;

public class Solution {

    public List<String> wordBreak(String s, List<String> wordDict) {
        // 为了快速判断一个单词是否在单词集合中，需要将它们加入哈希表
        Set<String> wordSet = new HashSet<>(wordDict);
        int len = s.length();

        // 第 1 步：动态规划计算是否有解
        // dp[i] 表示「长度」为 i 的 s 前缀子串可以拆分成 wordDict 中的单词
        // 长度包括 0 ，因此状态数组的长度为 len + 1
        boolean[] dp = new boolean[len + 1];
        // 0 这个值需要被后面的状态值参考，如果一个单词正好在 wordDict 中，dp[0] 设置成 true 是合理的
        dp[0] = true;

        for (int right = 1; right <= len; right++) {
            // 如果单词集合中的单词长度都不长，从后向前遍历是更快的
            for (int left = right - 1; left >= 0; left--) {
                // substring 不截取 s[right]，dp[left] 的结果不包含 s[left]
                if (wordSet.contains(s.substring(left, right)) && dp[left]) {
                    dp[right] = true;
                    // 这个 break 很重要，一旦得到 dp[right] = True ，不必再计算下去
                    break;
                }
            }
        }

        // 第 2 步：回溯算法搜索所有符合条件的解
        List<String> res = new ArrayList<>();
        if (dp[len]) {
            Deque<String> path = new ArrayDeque<>();
            dfs(s, len, wordSet, dp, path, res);
            return res;
        }
        return res;
    }

    /**
     * s[0:len) 如果可以拆分成 wordSet 中的单词，把递归求解的结果加入 res 中
     *
     * @param s
     * @param len     长度为 len 的 s 的前缀子串
     * @param wordSet 单词集合，已经加入哈希表
     * @param dp      预处理得到的 dp 数组
     * @param path    从叶子结点到根结点的路径
     * @param res     保存所有结果的变量
     */
    private void dfs(String s, int len, Set<String> wordSet, boolean[] dp, Deque<String> path, List<String> res) {
        if (len == 0) {
            res.add(String.join(" ",path));
            return;
        }

        // 可以拆分的左边界从 len - 1 依次枚举到 0
        for (int i = len - 1; i >= 0; i--) {
            String suffix = s.substring(i, len);
            if (wordSet.contains(suffix) && dp[i]) {
                path.addFirst(suffix);
                dfs(s, i, wordSet, dp, path, res);
                path.removeFirst();
            }
        }
    }
}

实际上上面代码的 dfs 过程中不加 dp[i] 也是可以过的，这个问题中动态规划的主要作用是帮助评估是否有解来进行剪枝

这个是自己用回溯实现的代码，跑出来效率比较差，一开始没加动态规划进行剪枝，碰到没有解的用例就跑超时了，看了题解后加上了动态规划来剪枝，代码才跑通，感觉这个代码实现的还挺蠢，没想到可以把单词列表中所有单词加入到HashSet 中，还有就是看题解后才知道还有 String.join() 这个将列表中字符串拼接起来的方法，以及如果单词集合中的单词长度都不长，从后向前遍历是更快的，感觉从这题中学习到的东西还是挺多的

import java.util.*;

class Solution {
    List<String> res = new ArrayList<>();
    StringBuilder temp = new StringBuilder();
    int max = 0;
    int len = 0;
    int con = 0;

    public List<String> wordBreak(String s, List<String> wordDict) {
        len = s.length();
        HashSet<String> wordSet = new HashSet<>(wordDict);
        Map<Integer, List<String>> map = new HashMap<>();
        StringBuilder sb = new StringBuilder(s);
        for (String word : wordDict) {
            int len = word.length();
            max = Math.max(len, max);
            if (map.containsKey(len)) {
                map.get(len).add(word);
            } else {
                List<String> cur = new ArrayList<>();
                cur.add(word);
                map.put(len, cur);
            }
        }
        boolean[] dp = new boolean[len + 1];
        dp[0] = true;
        for (int i = 1; i <= len; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if (wordSet.contains(s.substring(j, i)) && dp[j]) {
                    dp[i] = true;
                    break;
                }
            }
        }
        if (!dp[len]) return res;
        dfs(sb, s, map, 0);
        return res;
    }

    private void dfs(StringBuilder sb, String s, Map<Integer, List<String>> map, int index) {
        if (index >= len) {
            sb.deleteCharAt(sb.length() - 1);
            res.add(sb.toString());
            sb.insert(sb.length(), " ");
            return;
        }
        for (int i = 1; i <= max; i++) {
            if (index + i  - 1 < len) {
                String cur = s.substring(index, index + i);
                if (map.containsKey(i)) {
                    
                    for (String ss : map.get(i)) {
                        if (ss.equals(cur)) {
                            int pre = index + i + con;
                            sb.insert(pre, " ");
                            con++;
                            dfs(sb, s, map,index + i);
                            sb.deleteCharAt(pre);
                            con--;
                        }
                    }
                }
            }
        }
    }
}