罗马数字转整数

发表于 更新于
本文字数： 2.2k 阅读时长 ≈ 2 分钟

LeetCode题目，13. Roman to Integer

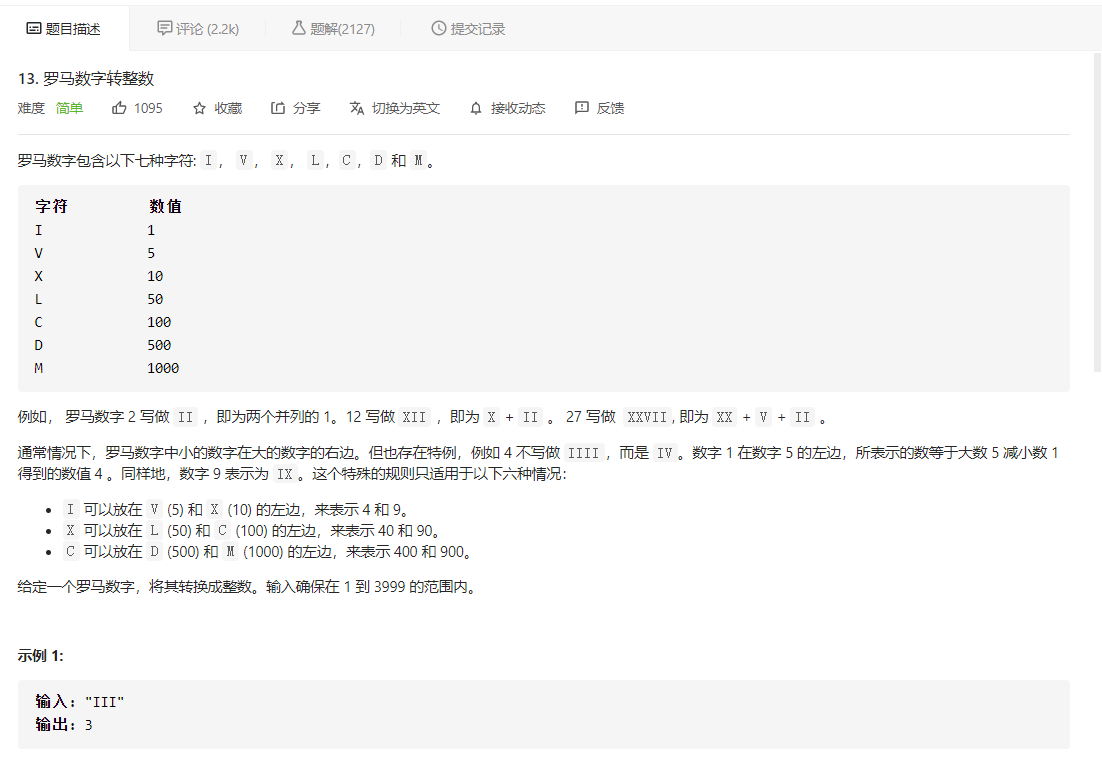
先看题目描述

B1Oawj.png

大意就是给定一个罗马数字，将其转成整数

算法和思路

第一时间想到的思路是用两个数组按照降序分别存储罗马数字和其对应的整数，然后用一个指针 i 来遍历字符串，用一个 index 指针来指向数组存储的罗马数字，每次都看子串 s[i, i + 1] 或 s[i, i] 是否与 index 指向的罗马数字相等，若都不想等的话，则移动 index 指针直至相等；若相等的话，则加上该罗马数字的对应的整数，然后将 i 指针向右移动一位或两位

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int romanToInt(String s) {
        String[] ss = new String[]{"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
        int[] nums = new int[]{1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
        int res = 0;
        int index = 0;
        int len = s.length();
        int i = 0;
        while (i < len) {
            if (i < len - 1 && s.substring(i, i + 2).equals(ss[index])) {
                res += nums[index];
                i += 2;
            } else if (s.substring(i, i+ 1).equals(ss[index])) {
                res += nums[index];
                i++;
            } else {
                index++;
            }
        }
        return res;
    }
}

但这个算法的运行效率较低，后来去看题解，发现可以总结出如下规则：

  • 罗马数字由 I,V,X,L,C,D,M 构成；
  • 当小值在大值的左边，则减小值，如 IV=5-1=4；
  • 当小值在大值的右边，则加小值，如 VI=5+1=6；
  • 由上可知，右值永远为正，因此最后一位必然为正

在代码实现上，可保留当前位的值，当遍历到下一位的时，对比保留值与遍历位的大小关系，再确定保留值为加还是减。最后一位做加法即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    public int romanToInt(String s) {
        int res = 0;
        int pre = getValue(s.charAt(0));
        for(int i = 1; i < s.length(); i ++) {
            int cur = getValue(s.charAt(i));
            if(pre < cur) {
                res -= pre;
            } else {
                res += pre;
            }
            pre = cur;
        }
        res += pre;
        return res;
    }

    private int getValue(char ch) {
        switch(ch) {
            case 'I': return 1;
            case 'V': return 5;
            case 'X': return 10;
            case 'L': return 50;
            case 'C': return 100;
            case 'D': return 500;
            case 'M': return 1000;
            default: return 0;
        }
    }
}

还有一个十分有趣的地方：这里的代码中得到罗马数字对应的整数使用了 switch 语句，其实使用哈希表也可以，但使用哈希表的效率会明显低于 switch 语句，可能是因为小数据量下哈希表体现不出速度优势