整数转罗马数字

发表于
本文字数： 2.5k 阅读时长 ≈ 2 分钟

LeetCode题目，12. Integer to Rooman

先看题目描述

BPwCJe.png

大意就是给定一个整数，让我们将其转为罗马数字

算法和思路

哈希表

大致思路就是先用一个哈希表将各整数对应的罗马数字储存起来，然后从左到右一层层的转化为罗马数字

算法流程如下：

  • 先计算出整数的长度 len
  • 令 i 从 len - 1 到 0 进行 len -1 次循环：
    • 令 con 等于 10 的 len - 1 次方，cur = num / con
    • 若 cur 等于 4 或 9，则直接在 res 后添加 con × cur 对应的罗马字符
    • 否则：
      • 若 cur 大于等于 5，则先在 res 后添加 con × 5 对应的罗马字符，再将 cur - 5
      • 在 res 后添加 cur 个 con 对应的罗马字符
    • num = num % con
  • 最终返回 res

贪心算法

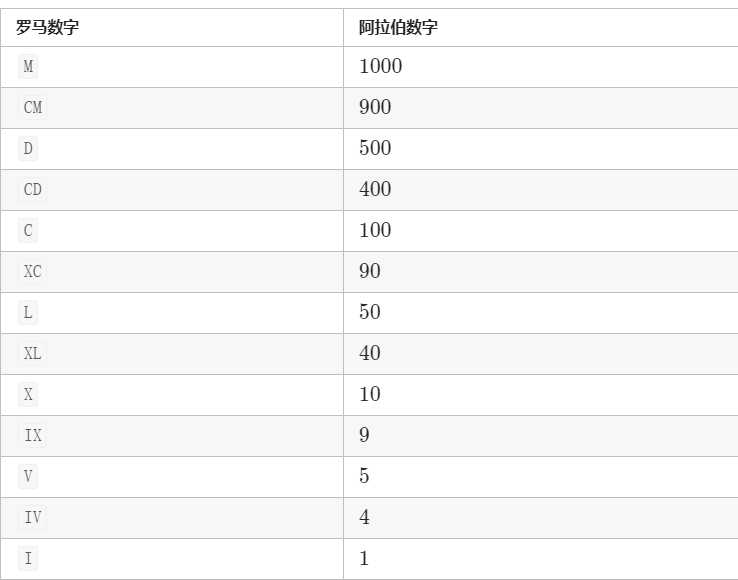
这题的背景类似找零钱问题，罗马数字与阿拉伯数字的对应关系从大到小排列如下图所示

BPBgRe.png

于是，“将整数转换为罗马数字”的过程，就是用上面这张表中右边的数字作为“加法因子”去分解一个整数，目的是“分解的整数个数”尽可能少，因此，对于这道问题，类似于用最少的纸币凑成一个整数，贪心算法的规则如下：

每一步都使用当前较大的罗马数字作为加法因子，最后得到罗马数字表示就是长度最少的。

算法源码

哈希表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import java.util.*;

class Solution {
    private HashMap<Integer, String> map = new HashMap<Integer, String>();

    public String intToRoman(int num) {
        map.put(1, "I");
        map.put(5, "V");
        map.put(10, "X");
        map.put(50, "L");
        map.put(100, "C");
        map.put(500, "D");
        map.put(1000, "M");
        map.put(4, "IV");
        map.put(9, "IX");
        map.put(40, "XL");
        map.put(90, "XC");
        map.put(400, "CD");
        map.put(900, "CM");
        StringBuilder res = new StringBuilder();
        int temp = num;
        int len = 0;
        while (temp != 0) {
            temp /= 10;
            len++;
        }
        for (int i = len - 1; i >= 0; i--) {
            int con = (int)Math.pow(10, i);
            int cur = num / con;
            if (cur % 5 == 4) {
                res.append(map.get(con * cur));
            } else {
                if (cur >= 5) {
                    res.append(map.get(con * 5));
                    cur = cur - 5;
                }
                for (int j = 0; j < cur; j++) {
                    res.append(map.get(con));
                }
            }
            num = num % con;
        }
        return res.toString();
    }
}

贪心算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public String intToRoman(int num) {
        StringBuilder res = new StringBuilder();
        // 把阿拉伯数字与罗马数字可能出现的所有情况和对应关系，放在两个数组中
        // 并且按照阿拉伯数字的大小降序排列，这是贪心选择思想
        int[] nums = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
        String[] romans = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
        int index = 0;
        while (index < 13) {
            while (num >= nums[index]) {
                res.append(romans[index]);
                num -= nums[index];
            }
            index++;
        }
        return res.toString();
    }
}