N皇后

发表于
本文字数： 2.1k 阅读时长 ≈ 2 分钟

LeetCode题目，51. N-Queens

先看题目描述

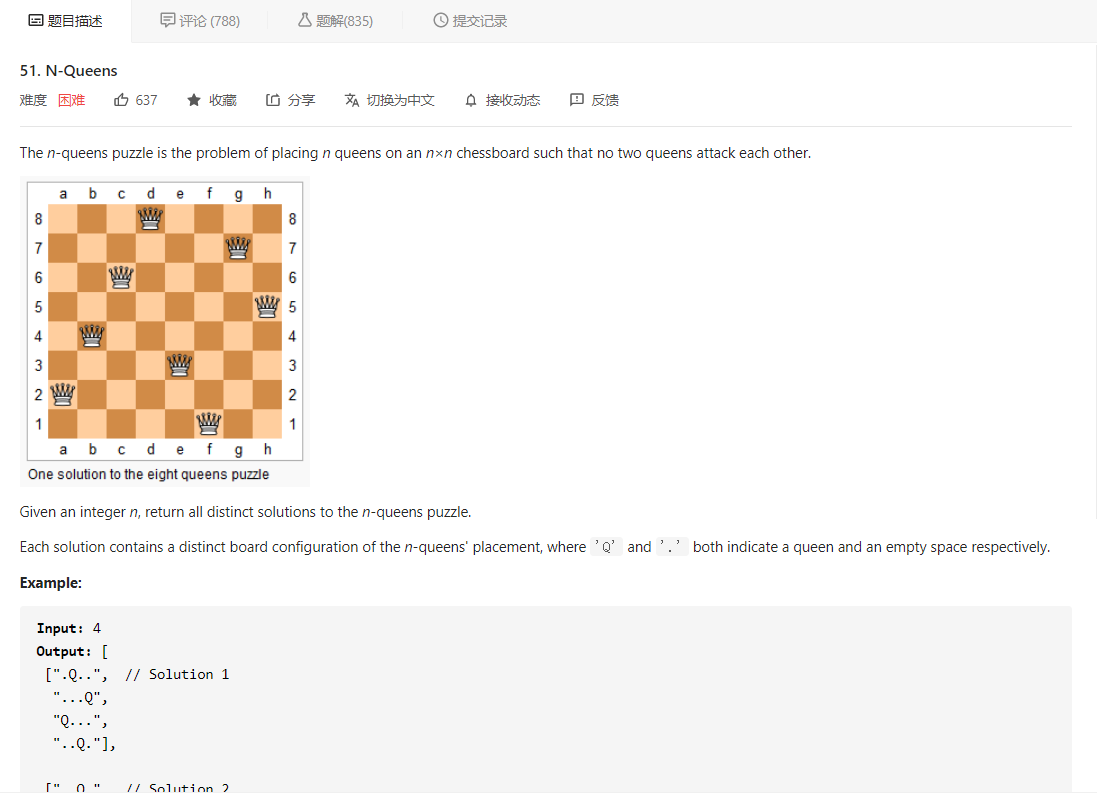
n 皇后问题研究的是如何将 n 个皇后放在一个 n × n 的棋盘上，并且使皇后不能彼此之间相互攻击，皇后的攻击方式是可以走直线攻击，也可以走对角线斜着攻击。题目要求是给定一个 n 代表皇后数量，让我们返回所有不同的 n 皇后问题的解决方案

算法和思路

回溯搜索算法(深度优先遍历).

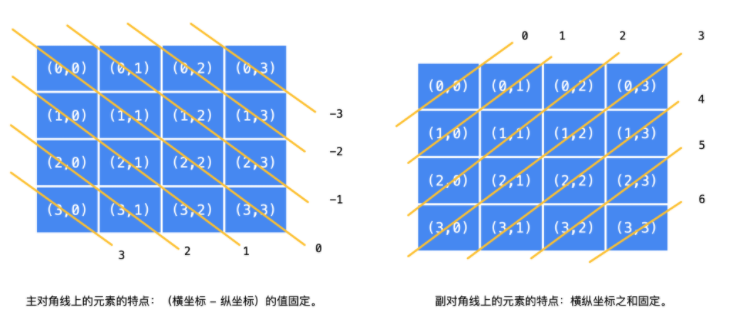
思路就是尝试一行行的摆皇后位置，由于要保证皇后不能同时出现在 同一主对角线方向 或者 同一副对角线方向 或者同一列上，我们要为每一列，主对角线和副对角线设置相应的布尔数组变量，只要排定了某个皇后的位置，就要将其位置那列，主对角线和副对角线对应的布尔变量设置为 true，表示占住了对应的位置；当排定了某一行的皇后时，就去排下一行的皇后，只要「检测」到新摆放的「皇后」与已经摆放好的「皇后」冲突，就尝试摆放同一行的下一个位置，到行尾还不能放置皇后，就执行回溯操作

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import java.util.*;

class Solution {
    List<List<String>> res = new ArrayList<>();
    private Deque<Integer> path;
    private boolean[] cols;
    private boolean[] main;
    private boolean[] sub;

    public List<List<String>> solveNQueens(int n) {
        path = new LinkedList<>();
        res = new ArrayList<>();
        if (n == 0) return res;
        cols = new boolean[n];
        main = new boolean[2 * n - 1];
        sub = new boolean[2 * n - 1];
        dfs(0, n);
        return res;
    }

    private void dfs(int row, int n) {
        if (row == n) {
            List<String> board = convertToBoard(path, n);
            res.add(board);
            return;
        }
        for (int i = 0; i < n; i++) {
            if (!cols[i] && !main[row + i] && !sub[row - i + n - 1]) {
                cols[i] = true;
                main[row + i] = true;
                sub[row - i + n - 1] = true;
                path.add(i);
                dfs(row + 1, n);
                path.removeLast();
                cols[i] = false;
                main[row + i] = false;
                sub[row - i + n - 1] = false;
            }
        }
    }

    private List<String> convertToBoard(Deque<Integer> path, int n) {
        List<String> board = new ArrayList<>();
        for (int num : path) {
            StringBuilder temp = new StringBuilder();
            temp.append(".".repeat(n));
            temp.replace(num, num + 1, "Q");
            board.add(temp.toString());
        }
        return board;
    }
}