LeetCode每日一题,200. Number of Islands
先看题目描述
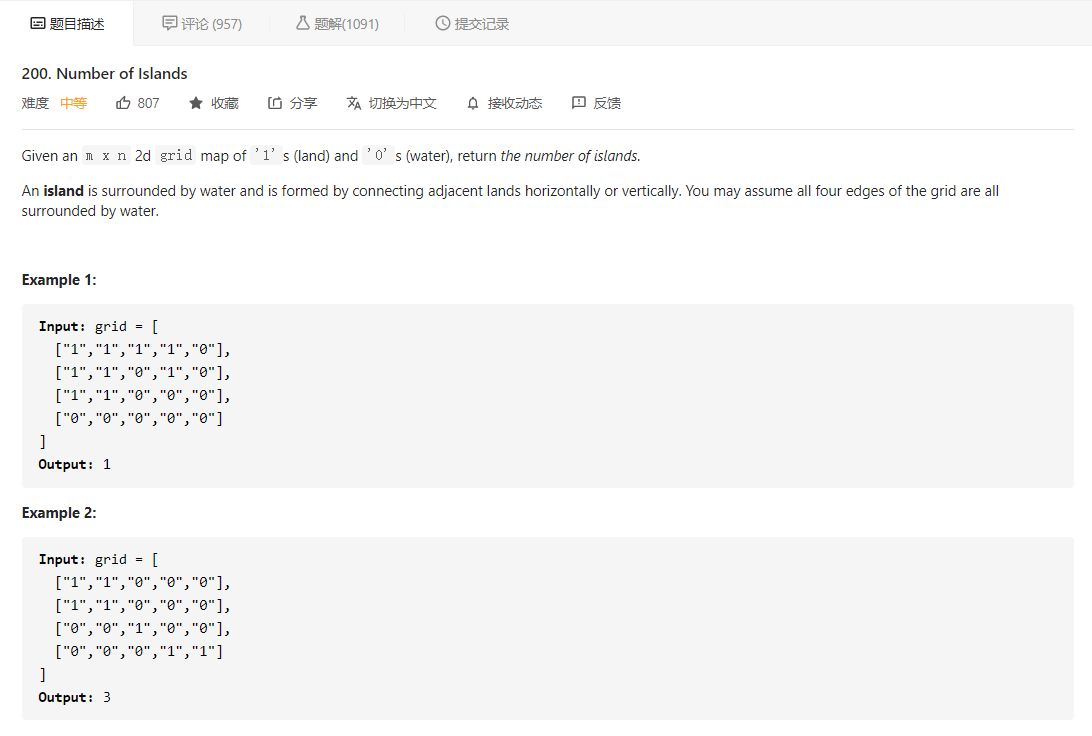
大意就是给定一个二维网格,代表岛屿地图,网格中 ‘1’ 代表岛屿,’0’ 代表海,让我们返回岛屿地图中的群岛数量
算法和思路
深度优先搜索
定义一个 visited 数组来记录某个岛是否已被访问过,扫描整个二维网格,如果一个位置为 1 且未被访问过,则从此点开始j进行深度优先搜索,在深度优先搜索过程中,每个搜索到的未被访问的岛屿都会被标记为 visited,最终群岛的数量就是深度优先搜索的次数
算法源码
深度优先搜索
1 | class Solution { |
后面看题解还看到了个并查集的解法,感觉很新奇,因为以前只做过一道用并查集解决的题目,接触并查集不多
并查集
1 | public class Solution { |