不同的二叉搜索树II

LeetCode题目，95. Convert BST to Greater Tree

先看题目描述

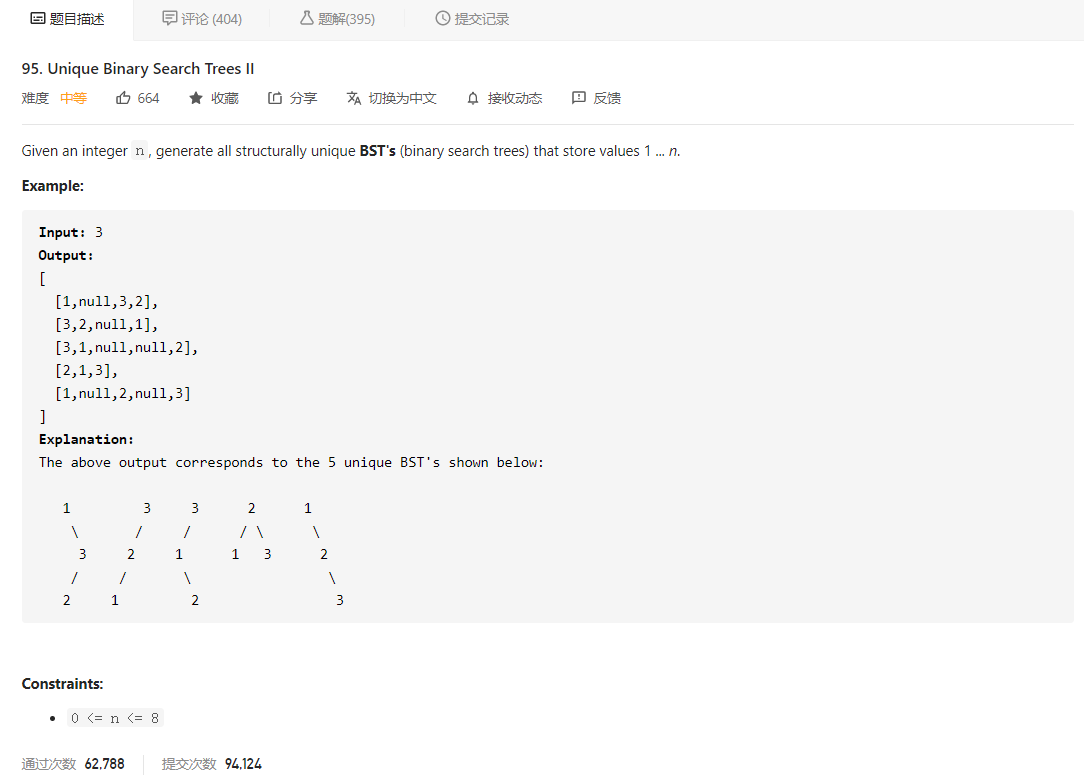
大意就是给定一个数字 N，返回所有存储数字 1..N 的二叉搜索树

算法和思路

二叉搜索树关键的性质是根节点的值大于左子树所有节点的值，小于右子树所有节点的值，且左子树和右子树也同样为二叉搜索树。因此在生成所有可行的二叉搜索树的时候，假设当前序列长度为 n，如果我们枚举当前根节点的值为 i，那么根据二叉搜索树的性质我们可以知道左子树的节点值的集合为[1, …, i - 1]，右子树的节点值的集合为[i + 1, …, n]。而左子树和右子树的生成相较于原问题是一个序列长度缩小的子问题，因此我们可以想到用递归的方法来解决这道题目

我们定义 generateTrees(start, end) 函数表示当前值的集合为 [start, end]，返回序列 [start, end] 生成的所有可行的二叉搜索树。按照上文的思路，我们考虑枚举 [start, end] 中的值 i 为当前二叉搜索树的根，那么序列划分为了[start, i - 1] 和 [i + 1, end] 两部分。我们递归调用这两部分，即 generateTrees(start, i - 1) 和 generateTrees(i + 1, end)，获得所有可行的左子树和可行的右子树，那么最后一步我们只要枚举左子树集合从可行左子树中选一棵，再枚举右子树集合从可行右子树中选一棵拼接到根节点上，并每次枚举时将生成的二叉搜索树放入答案数组即可

递归的入口即为 generateTrees(1, n)，出口为当 start>end 的时候，代表当前二叉搜索树为空，返回空节点即可

算法源码

import java.util.*;

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public  List<TreeNode> generateTrees(int n) {
        if (n == 0) return new ArrayList<TreeNode>();
        return generateTrees(1, n);
    }

    private List<TreeNode> generateTrees(int start, int end) {
        List<TreeNode> res = new ArrayList<TreeNode>();
        if (start > end) {
            res.add(null);
            return res;
        }
        for (int i = start; i <= end; i++) {
            List<TreeNode> leftTrees = generateTrees(start, i - 1);
            List<TreeNode> rightTrees = generateTrees(i + 1, end);
            for (TreeNode leftTree: leftTrees) {
                for (TreeNode rightTree: rightTrees) {
                    TreeNode root = new TreeNode(i);
                    root.left = leftTree;
                    root.right = rightTree;
                    res.add(root);
                }
            }
        }
        return res;
    }
}