树中距离之和

LeetCode每日一题，834. Sum of Distances in Tree

先看题目描述

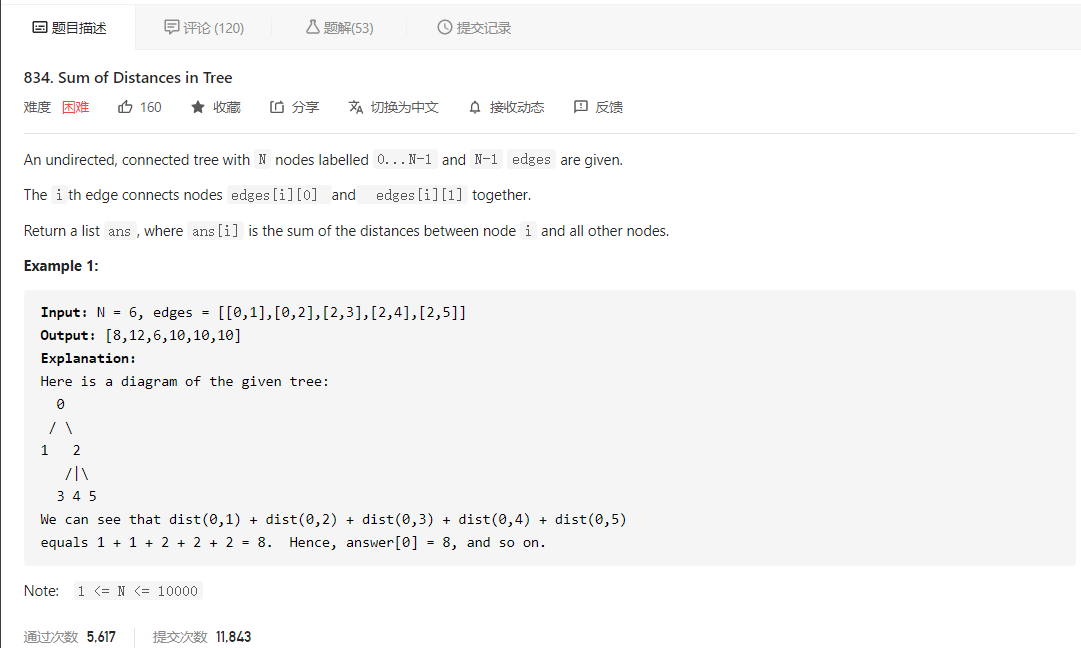
大意就是给定一个无向连通的树，数种有 N 个被标记为 0 … N - 1 的节点以及 N - 1 条边，返回一个表示每个节点与其他所有节点距离之和的列表 ans

算法和思路

树形动态规划

首先我们来考虑一个节点的情况，即每次题目指定一棵树，以 \textit{root}root 为根，询问节点 \textit{root}root 与其他所有节点的距离之和。

很容易想到一个树形动态规划：定义 dp[u] 表示以 u 为根的子树，它的所有子节点到它的距离之和，同时定义 sz[u] 表示以 u 为根的子树的节点数量，不难得出如下的转移方程：

$$dp[u] = \sum_{v∈son[u]}(dp[v] + sz[v])$$

其中 son[u] 表示 uu 的所有后代节点集合。转移方程表示的含义就是考虑每个后代节点 v，已知 v 的所有子节点到它的距离之和为 dp[v]，那么这些节点到 u 的距离之和还要考虑 u→v 这条边的贡献。考虑这条边长度为 1，一共有 sz[v] 个节点到节点 u 的距离会包含这条边，因此贡献即为 $1 × sz[v] = sz[v]$。我们遍历整棵树，从叶子节点开始自底向上递推到根节点 root 即能得出最后的答案为 dp[root]

经过一次树形动态规划后其实我们获得了在 uu 为根的树中，每个节点为根的子树的答案 \textit{dp}dp，我们可以利用这些已有信息来优化时间复杂度。

假设 u 的某个后代节点为 v，如果要算 v 的答案，本来我们要以 v 为根来进行一次树形动态规划。但是利用已有的信息，我们可以考虑树的形态做一次改变，让 v 换到根的位置，u 变为其孩子节点，同时维护原有的 dp 信息。在这一次的转变中，我们观察到除了 u 和 v 的 dp 值，其他节点的 dp 值都不会改变，因此只要更新 dp[u] 和 dp[v] 的值即可。

那么我们来看 v 换到根的位置的时候怎么利用已有信息求出 dp[u] 和 dp[v] 的值。重新回顾第一次树形动态规划的转移方程，我们可以知道当 u 变为 v 的孩子的时候 v 不在 u 的后代集合 son[u] 中了，因此此时 dp[u] 需要减去 v 的贡献，同时 sz[u] 也要相应减去 sz[v]，即

$$dp[u] = dp[u] - (dp[v] + sz[v])$$

$$sz[u] = sz[u] - sz[v]$$

而 v 的后代节点集合中多出了 u，因此 dp[v] 的值要由 u 更新上来，同时 sz[v] 也要相应加上 sz[u]，即

$$dp[v] = dp[v] + (dp[u] + sz[u])$$

$$sz[v] = sz[v] + sz[u]$$

至此我们完成了一次换根操作，在 O(1) 的时间内维护了 dp 的信息，且此时的树结构以 v 为根。那么接下来我们不断地进行换根的操作，即能在 O(N) 的时间内求出每个节点为根的答案

算法源码

在换根的过程中，我们是要对根节点的每一个子节点进行换根，但我们实际上对每个节点维护的邻居节点里，除了子节点以外，是还包含一个父节点的，所以在遍历邻居节点进行换根操作时，父节点是要跳过的。两种方法都可以实现这个，一种是维护一个布尔数组 visited 来记录哪些节点已经访问过，即执行过换根操作；另一种是在深度优先遍历树的过程中，记录下当前节点的父节点，遍历邻居节点时遇见父节点就跳过，第二种的效率略优于第一种

第一种

import java.util.*;

class Solution {
    private List<List<Integer>> graph = new ArrayList<List<Integer>>();
    private int[] dp;
    private int[] sz;
    private int[] ans;
    private boolean[] visited;

    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        dp = new int[N];
        sz = new int[N];
        ans = new int[N];
        visited = new boolean[N];
        for (int i = 0; i < N; i++) {
            graph.add(new ArrayList<>());
        }
        for (int[] edge: edges) {
            graph.get(edge[0]).add(edge[1]);
            graph.get(edge[1]).add(edge[0]);
        }
        dfs1(0);
        visited = new boolean[N];
        dfs2(0);
        return ans;
    }

    private void dfs1(int index) {
        visited[index] = true;
        dp[index] = 0;
        sz[index] = 1;
        for (int node: graph.get(index)) {
            if (visited[node]) {
                continue;
            }
            dfs1(node);
            dp[index] += dp[node] + sz[node];
            sz[index] += sz[node];
        }
    }

    private void dfs2(int index) {
        ans[index] = dp[index];
        visited[index] = true;
        for (int node: graph.get(index)) {
            if (visited[node]) {
                continue;
            }
            int pu = dp[index];
            int su = sz[index];
            int pv = dp[node];
            int sv = sz[node];
            dp[index] -= dp[node] + sz[node];
            sz[index] -= sz[node];
            dp[node] += dp[index] + sz[index];
            sz[node] += sz[index];
            dfs2(node);
            dp[index] = pu;
            sz[index] = su;
            dp[node] = pv;
            sz[node] = sv;
        }
    }
}

第二种

import java.util.*;

class Solution {
    private int[] ans;
    private int[] sz;
    private int[] dp;
    private List<List<Integer>> graph = new ArrayList<List<Integer>>();

    public int[] sumOfDistancesInTree(int N, int[][] edges) {
        dp = new int[N];
        sz = new int[N];
        ans = new int[N];
        for (int i = 0; i < N; i++) {
            graph.add(new ArrayList<>());
        }
        for (int[] edge: edges) {
            graph.get(edge[0]).add(edge[1]);
            graph.get(edge[1]).add(edge[0]);
        }
        dfs1(0, -1);
        dfs2(0, -1);
        return ans;
    }

    private void dfs1(int index, int pre) {
        dp[index] = 0;
        sz[index] = 1;
        for (int node: graph.get(index)) {
            if (node == pre) {
                continue;
            }
            dfs1(node, index);
            dp[index] += dp[node] + sz[node];
            sz[index] += sz[node];
        }
    }

    private void dfs2(int index, int pre) {
        ans[index] = dp[index];
        for (int node: graph.get(index)) {
            if (node == pre) {
                continue;
            }
            int pu = dp[index];
            int su = sz[index];
            int pv = dp[node];
            int sv = sz[node];
            dp[index] -= dp[node] + sz[node];
            sz[index] -= sz[node];
            dp[node] += dp[index] + sz[index];
            sz[node] += sz[index];
            dfs2(node, index);
            dp[index] = pu;
            sz[index] = su;
            dp[node] = pv;
            sz[node] = sv;
        }
    }
}