LCP19 秋叶收藏集

发表于
本文字数： 1.7k 阅读时长 ≈ 2 分钟

LeetCode每日一题，LCP 19. 枫叶收藏集

先看题目描述

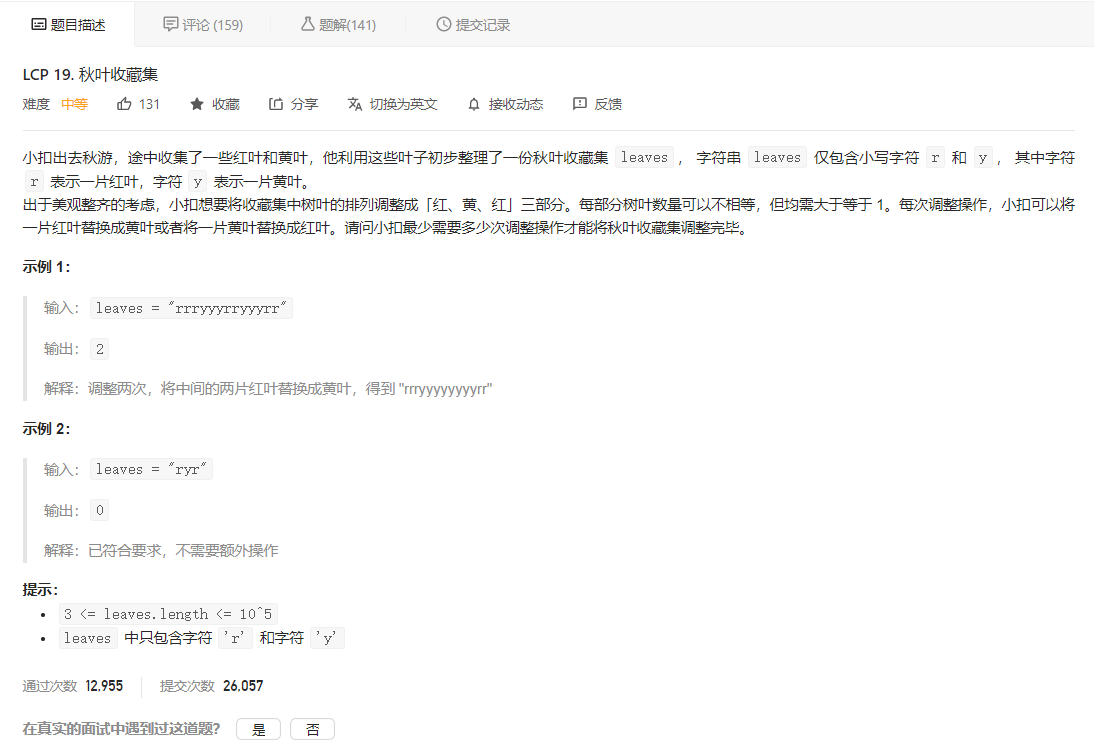
算法与思路

动态规划

由于我们想要将收藏集中树叶的排列调整成「红、黄、红」三部分，因此我们可以用 3个状态分别表示其中的每一部分，即状态 0 和状态 2 分别表示前面和后面的红色部分，状态 1 表示黄色部分

此时，我们就可以尝试使用动态规划解决本题了。我们用 dp[i][j] 表示对于第 0 片到第 i 片叶子（记为 leaves[0..i]）进行调整操作，并且第 i 片叶子处于状态 j 时的最小操作次数。在推导状态转移方程时，我们可以分别对于每一种状态进行分析。

  • 当 j = 0 时，我们需要将第 i 片叶子变成红色，并且第 i−1 片叶子也只能处于 j=0 的状态（因为没有编号更小的状态了），因此有状态转移方程： dp[i][0] = dp[i - 1][0] + isYellow(i)
    其中 isYellow(i) 为示性函数，当第 i 片叶子为黄色时为 1，红色时为 0
  • 当 j = 1 时，我们需要将第 i 片叶子变成黄色，而第 i−1 片叶子既可以处于 j=1 的状态，也可以处于 j=0 的状态，我们选择其中的较小值，因此有状态转移方程： dp[i][1] = min(dp[i - 1][0], dp[i - 1][1]) + isRed(i)
    其中 isRed(i) 为示性函数，当第 i 片叶子为红色时为 1，黄色时为 0
  • 当 j = 2 时，我们需要将第 i 片叶子变成红色，而第 i−1 片叶子即可以处于 j=2 的状态，也可以处于 j=1 的状态（注意这里不能处于 j=0 的状态，因为每一种状态包含的叶子数量必须至少为 1），我们选择其中的较小值，因此有状态转移方程：dp[i][2] = min(dp[i - 1][1], dp[i - 1][2]) + isYellow(i)

最后返回 dp[n-1][2] 即可，其中 n 是字符串 leaves 的长度，也就是树叶的总数

注意：考虑边界情况，当 i = 0 时，叶子只有 0 一种状态；当 i = 1 时，叶子只有 0 和 1 两种状态；当 $i \geq 2$ 时，叶子才存在0， 1， 2三种状态

算法源码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minimumOperations(String leaves) {
        int n = leaves.length();
        int[][] dp = new int[leaves.length()][3];
        dp[0][0] = leaves.charAt(0) == 'y' ? 1 : 0;
        dp[0][1] = dp[0][2] = dp[1][2] = Integer.MAX_VALUE;
        for (int i = 1; i < n; i++) {
            int isRed = leaves.charAt(i) == 'r' ? 1 : 0;
            int isYellow = leaves.charAt(i) == 'y' ? 1 : 0;
            dp[i][0] = dp[i - 1][0] + isYellow;
            dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][1]) + isRed;
            if (i > 1) {
                dp[i][2] = Math.min(dp[i - 1][1], dp[i - 1][2]) + isYellow;
            }
        }
        return dp[n - 1][2];
    }
}