填充每个节点的下一个右侧节点

LeetCode每日一题，117. Populating Next Right Pointers in Each Node II

先看题目描述

大意就是给定一棵二叉树，让我们把里面每个节点的 next 指针指向其右侧的第一个节点

算法思路

BFS

由于这道题要的是把二叉树的每一行都串联起来，那么使用 BFS 来进行层次遍历就很合适，在遍历每一层时，让前一个节点的 next 指针指向当前节点即可

DFS

使用 DFS 来进行先根遍历，中根遍历或后根遍历都可以，只要保证是先遍历的左子树再遍历右子树就行，使用一个 HashMap 来存储当前遍历的某个深度对应的最右节点，在遍历到某个节点时，若 HashMap 的 key 中不存在当前深度，那么这个节点就是该深度的最左节点，将深度和该节点作为键值对添加到 HashMap 中；若 HashMap 的 key 中存在当前深度，那么此时该 key 值对应的 value 就是目前该深度的最右节点，令这个节点的 next 指针指向当前遍历的节点，再将该 key 值对应的 value 置为当前遍历的节点。遍历完后返回 root 即可

迭代

我们可以把每一行都看成一个链表，我们设置个 cur 看作是当前层的链表，设置个哑节点 flag 作为下一层的链表头，通过遍历当前层链表的节点来将下一层串联起来。将下一层串联成一个链表后，将 flag.next 赋值给 cur，后续继续遍历循环，直到 cur 为空为止。迭代完后返回 root 即可

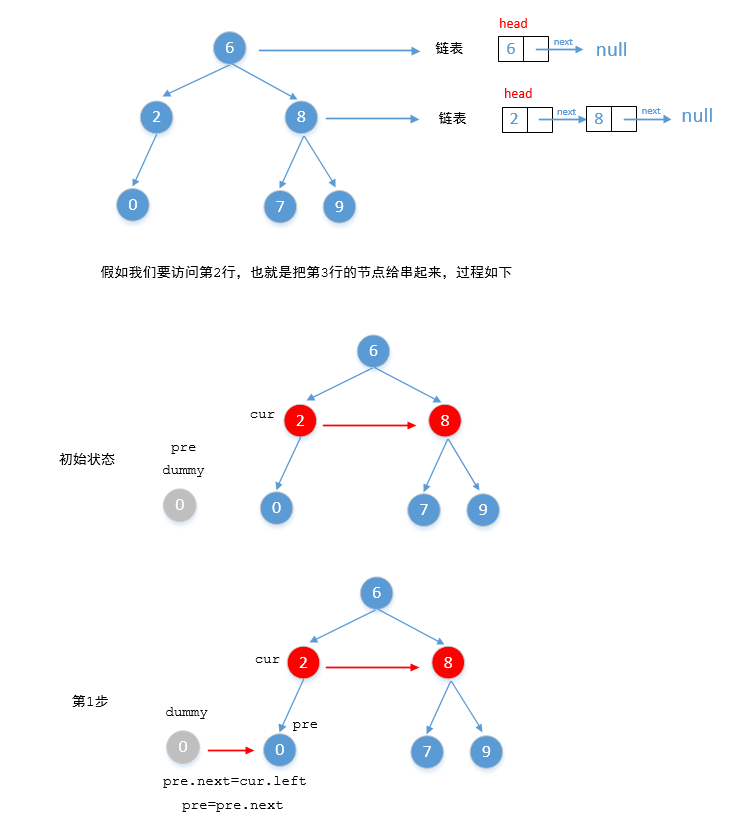
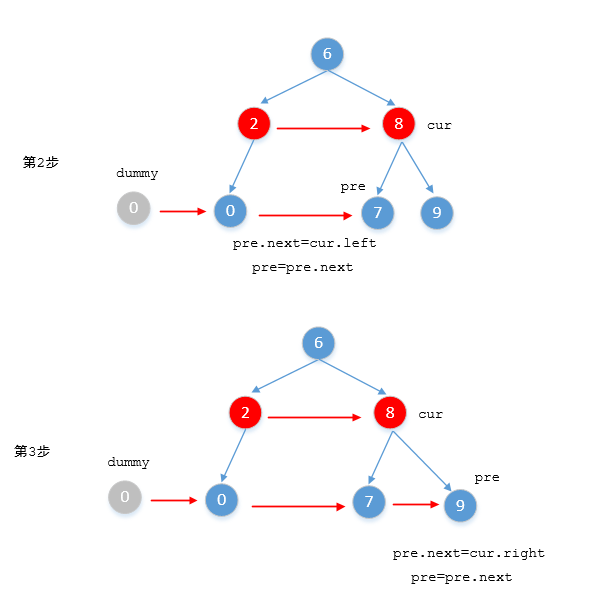
算法思路

BFS

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

import java.util.LinkedList;
import java.util.Queue;

class Solution {
    public Node connect(Node root) {
        if (root == null) return root;
        Queue<Node> queue = new LinkedList<Node>();
        queue.add(root);
        while (!queue.isEmpty()) {
            int con = queue.size();
            Node pre = null;
            for (int i = 0; i < con; i++) {
                Node node = queue.poll();
                if (pre != null) pre.next = node;
                pre = node;
                if (node.left != null) queue.add(node.left);
                if (node.right != null) queue.add(node.right);
            }
        }
        return root;
    }
}

DFS

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

import java.util.HashMap;
import java.util.Map;

class Solution {
    Map<Integer, Node> map = new HashMap<Integer, Node>();

    public Node connect(Node root) {
        if (root == null) return root;
        dfs(root, 0);
        return root;
    }
    
    private void dfs(Node root, int depth) {
        if (root == null) return;
        if (map.containsKey(depth)) map.get(depth).next = root;
        map.put(depth, root);
        dfs(root.left, depth + 1);
        dfs(root.right, depth + 1);
    }
}

迭代

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if (root == null)
            return root;
        //cur我们可以把它看做是每一层的链表
        Node cur = root;
        while (cur != null) {
            //遍历当前层的时候，为了方便操作在下一
            //层前面添加一个哑结点（注意这里是访问
            //当前层的节点，然后把下一层的节点串起来）
            Node dummy = new Node(0);
            //pre表示访下一层节点的前一个节点
            Node pre = dummy;
            //然后开始遍历当前层的链表
            while (cur != null) {
                if (cur.left != null) {
                    //如果当前节点的左子节点不为空，就让pre节点
                    //的next指向他，也就是把它串起来
                    pre.next = cur.left;
                    //然后再更新pre
                    pre = pre.next;
                }
                //同理参照左子树
                if (cur.right != null) {
                    pre.next = cur.right;
                    pre = pre.next;
                }
                //继续访问这一行的下一个节点
                cur = cur.next;
            }
            //把下一层串联成一个链表之后，让他赋值给cur，
            //后续继续循环，直到cur为空为止
            cur = dummy.next;
        }
        return root;
    }
}