组合 | Morichina

LeetCode每日一题，77. combination

先看题目描述

大意就是给定 n 和 k，让我们返回从 1 - n 中取 k 个数的所有组合情况

算法思路

这题刚开始不会，看了题解才发现这题和电话号码的字母组合类似，都可以套公式。使用回溯法，代码格式也近似

重点概括：

如果解决一个问题有多个步骤，每一个步骤有多种方法，题目又要我们找出所有的方法，可以使用回溯算法；
回溯算法是在一棵树上的深度优先遍历（因为要找所有的解，所以需要遍历）；
组合问题，相对于排列问题而言，不计较一个组合内元素的顺序性（即 [1, 2, 3] 与 [1, 3, 2] 认为是同一个组合），因此很多时候需要按某种顺序展开搜索，这样才能做到不重不漏。

回溯算法首先需要画出递归树，不同的树决定了不同的代码实现

既然是树形问题上的深度优先遍历，因此首先画出树形结构。例如输入：n = 4, k = 2，我们可以发现如下递归结构：

如果组合里有 1 ，那么需要在 [2, 3, 4] 里再找 1 个数；
如果组合里有 2 ，那么需要在 [3, 4] 里再找 1 个数。注意：这里不能再考虑 1，因为包含 1 的组合，在第 1 种情况中已经包含。

依次类推（后面部分省略），以上描述体现的递归结构是：在以 n 结尾的候选数组里，选出若干个元素。画出递归结构如下图：

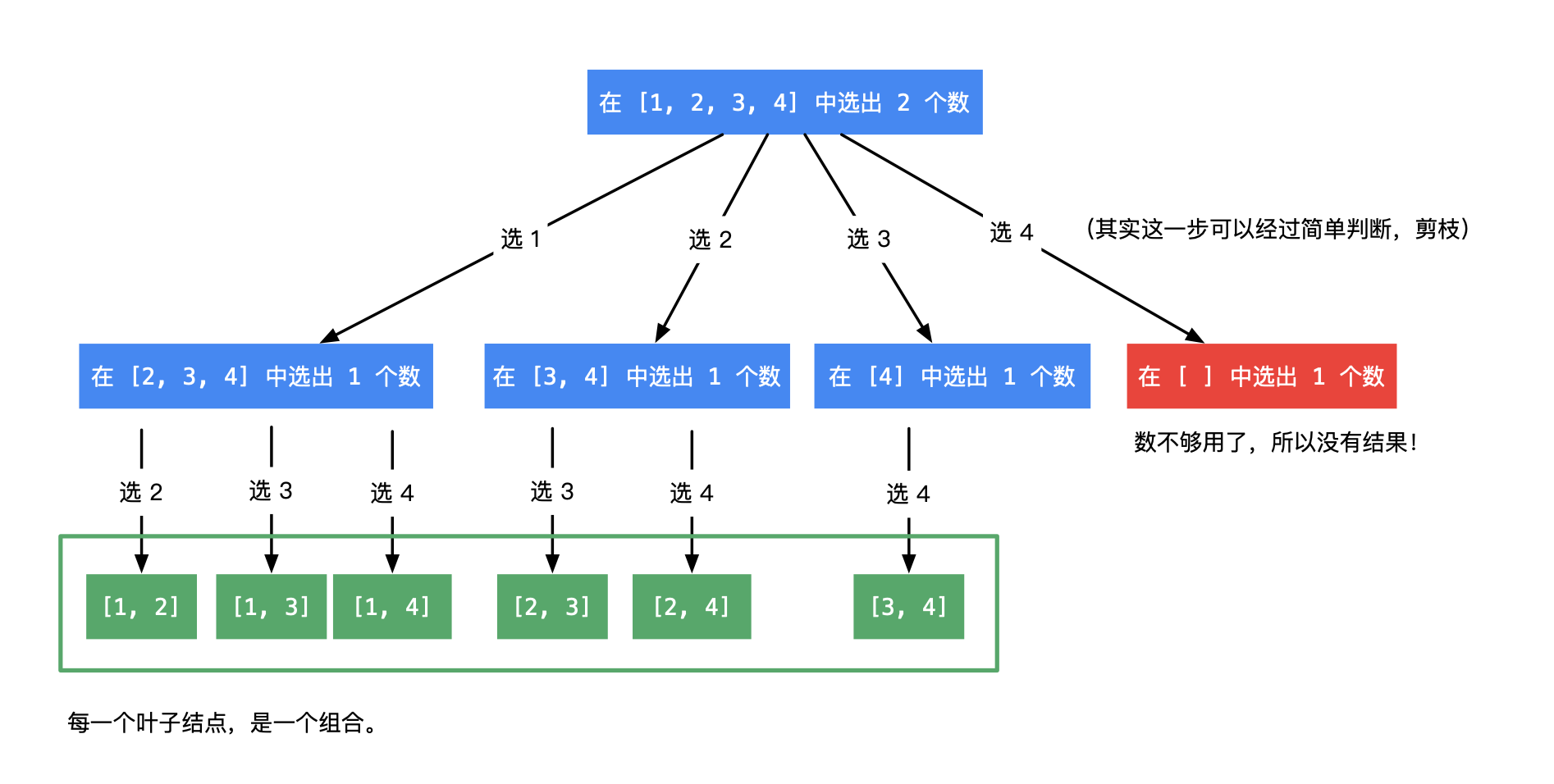
说明：

叶子结点的信息体现在从根结点到叶子结点的路径上，因此需要一个表示路径的变量 path，它是一个列表，特别地，path 是一个栈；
每一个结点递归地在做同样的事情，区别在于搜索起点，因此需要一个变量 start ，表示在区间 [begin, n] 里选出若干个数的组合；
有一些分支没有必要执行，可以进行剪枝

看了这个题解以后，再结合之前做的电话号码的字母组合这题，发现在刷题的过程中，除了做题和看题解之外，还需要时常进行归纳，有的同类型题目是有公式的，例如这两道题，都是组合问题，就可以使用回溯 + 剪枝来解题并优化，代码格式也十分相似

算法源码

import java.util.*;

class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<>();
        if (k > n || k < 0) return res;
        Deque<Integer> path = new ArrayDeque<>();
        dfs(n, k, 1, path, res);
        return res;
    }

    private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {
        if (path.size() == k) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i <= n - k + 1 + path.size(); i++) {
            path.add(i);
            dfs(n, k, i + 1, path, res);
            path.removeLast();
        }
    }
}