平衡二叉树

发表于
本文字数： 1.5k 阅读时长 ≈ 1 分钟

LeetCode每日一题，110. Balanced Binary Tree

先看题目描述

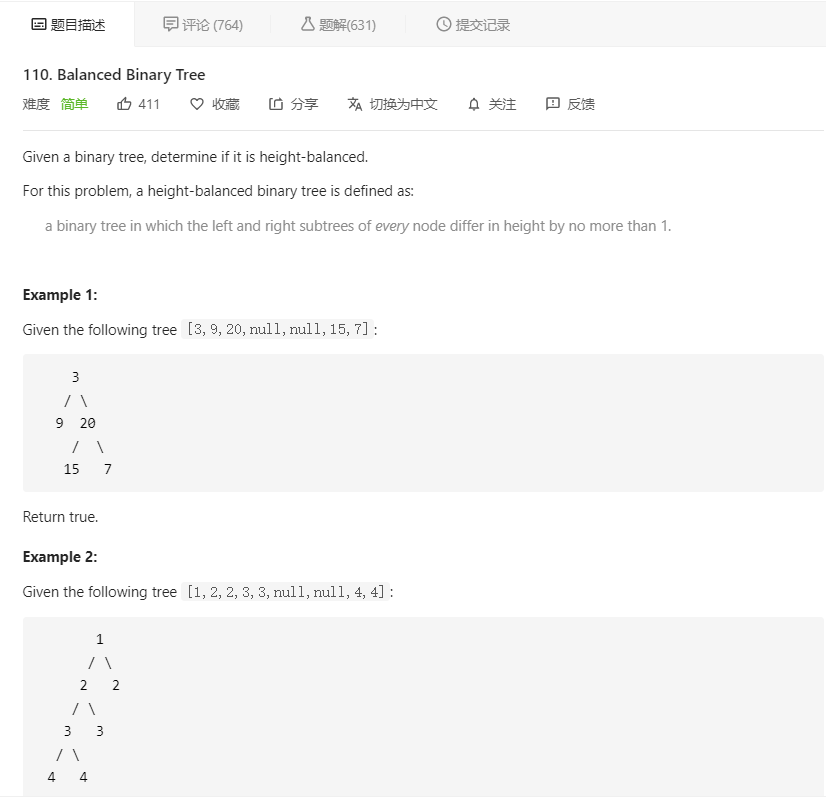
大意就是让我们判断一颗二叉树是否是平衡二叉树

算法思路

自顶向下

思路是构造一个计算二叉树深度的方法，通过比较此子树的左右子树的最大高度差，来判断当前子树是否是平衡二叉树，再去判断其左右子树是否是平衡二叉树，若树的所有子树都平衡，此树才平衡**

自底向上

这是看了题解才知道的方法，思路是对二叉树做先序遍历，自底向上返回子树最大高度，若判定某子树不是平衡树则 “剪枝” ，直接向上返回，这个方法代码的关键在于 recur 方法，既起到返回子树高度的作用，又起到体现子树是否平衡的作用。当 recur(root) 返回值为 -1 时，代表以 root 为根节点的子树不平衡，返回值为 0 时，代表 root 为空，返回值大于 0 时，则代表以 root 为根节点的子树平衡且返回的是该子树的高度

算法源码

自顶向下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) return true;
        return Math.abs(getDepth(root.left) - getDepth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }

    public int getDepth(TreeNode root) {
        if (root == null) return 0;
        return Math.max(getDepth(root.left), getDepth(root.right)) + 1;
    }
}

自底向上

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}